为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整)
|
组别 |
分数 |
人数 |
|
第1组 |
|
8 |
|
第2组 |
|
|
|
第3组 |
|
10 |
|
第4组 |
|
|
|
第5组 |
|
3 |
请根据以上信息,解答下列问题:
(1)求出 , 的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?

先化简,再求值: ,其中 .
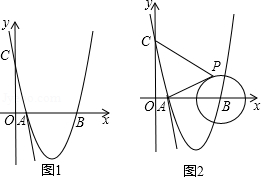
如图1,在平面直角坐标系中,直线 与 轴, 轴分别交于 , 两点,抛物线 经过 , 两点,与 轴的另一交点为 .
(1)求抛物线解析式及 点坐标;
(2)若点 为 轴下方抛物线上一动点,连接 、 、 ,当点 运动到某一位置时,四边形 面积最大,求此时点 的坐标及四边形 的面积;
(3)如图2,若 点是半径为2的 上一动点,连接 、 ,当点 运动到某一位置时, 的值最小,请求出这个最小值,并说明理由.
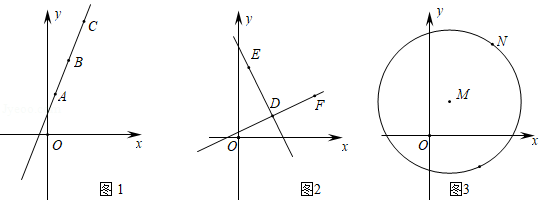
探究活动一:
如图1,某数学兴趣小组在研究直线上点的坐标规律时,在直线 上的三点 、 、 ,有 , ,发现 ,兴趣小组提出猜想:若直线 上任意两点坐
标 , , , ,则 是定值.通过多次验证和查阅资料得知,猜想成立, 是定值,并且是直线 中的 ,叫做这条直线的斜率.
请你应用以上规律直接写出过 、 两点的直线 的斜率 .
探究活动二
数学兴趣小组继续深入研究直线的“斜率”问题,得到正确结论:任意两条不和坐标轴平行的直线互相垂直时,这两条直线的斜率之积是定值.
如图2,直线 与直线 垂直于点 , , , .请求出直线 与直线 的斜率之积.
综合应用
如图3, 为以点 为圆心, 的长为半径的圆, , ,请结合探究活动二的结论,求出过点 的 的切线的解析式.
如图,在矩形 中,对角线 的中点为 ,点 , 在对角线 上, ,直线 绕点 逆时针旋转 角,与边 、 分别相交于点 、 (点 不与点 、 重合).
(1)求证:四边形 是平行四边形;
(2)若 , , ,求 的长.