探究活动一:
如图1,某数学兴趣小组在研究直线上点的坐标规律时,在直线上的三点、、,有,,发现,兴趣小组提出猜想:若直线上任意两点坐
标,,,,则是定值.通过多次验证和查阅资料得知,猜想成立,是定值,并且是直线中的,叫做这条直线的斜率.
请你应用以上规律直接写出过、两点的直线的斜率 .
探究活动二
数学兴趣小组继续深入研究直线的“斜率”问题,得到正确结论:任意两条不和坐标轴平行的直线互相垂直时,这两条直线的斜率之积是定值.
如图2,直线与直线垂直于点,,,.请求出直线与直线的斜率之积.
综合应用
如图3,为以点为圆心,的长为半径的圆,,,请结合探究活动二的结论,求出过点的的切线的解析式.
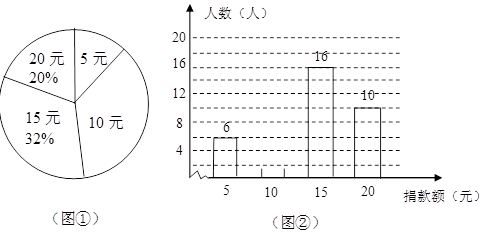
为支援“玉树抗震救灾”,在一次爱心捐款活动中,九(1)班同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元共四种情况.根据统计数据绘制了图①和图②两幅尚不完整的统计图.该班共有_____________名同学,学生捐款的众数是______________;
请你将图②的统计图补充完整;
计算该班同学平均捐款多少元?
从这个班任意抽取一名学生,这名学生捐款额为10元以上(不含10元)的概率是多少?
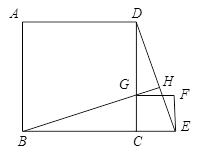
如图, 是同一直线上的三个点,四边形
是同一直线上的三个点,四边形 与四边形
与四边形 都是正方形,连结
都是正方形,连结 .
.观察图形,猜想
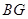 与
与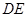 之间的大小关系,并证明你的结论;
之间的大小关系,并证明你的结论;若延长
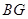 交
交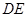 于点
于点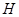 ,求证:
,求证: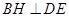 .
.
三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.
在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);
△BCD是不是黄金三角形,如果是,请给出证明;如果不是,请说明理由;
设
 ,试求k的值;
,试求k的值;如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,
请直接写出 的值.
的值.
已知二次函数的图象与x轴只有一个交点A(-2,0)、与y轴的交点为B(0,4),且其对称轴与y轴平行.求该二次函数的解析式,并在所给坐标系中画出它的大致图象;
在二次函数位于A、B两点之间的图象上取一点M,过点M分别作x轴、y轴的垂线,垂足分别为点C、D.求矩形MCOD的周长的最小值和此时的点M的坐标.

某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的 .
.求y与x之间的函数关系式;
由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.