(本小题满分13分)
已知抛物线 :
: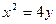 的焦点为
的焦点为 ,过点
,过点 作直线
作直线 交抛物线
交抛物线 于
于 、
、 两点;椭圆
两点;椭圆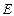 的中心在原点,焦点在
的中心在原点,焦点在 轴上,点
轴上,点 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率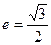 .
.
(1)求椭圆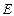 的方程;
的方程;
(2)经过 、
、 两点分别作抛物线
两点分别作抛物线 的切线
的切线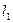 、
、 ,切线
,切线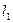 与
与 相交于点
相交于点 .证明:
.证明: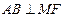 ;
;
(3) 椭圆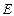 上是否存在一点
上是否存在一点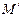 ,经过点
,经过点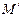 作抛物线
作抛物线 的两条切线
的两条切线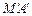 、
、 (
(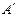 、
、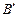 为切点),使得直线
为切点),使得直线 过点
过点 ?若存在,求出抛物线
?若存在,求出抛物线 与切线
与切线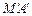 、
、 所围成图形的面积;若不存在,试说明理由
所围成图形的面积;若不存在,试说明理由 .
.
(本小题满分14分)给定正奇数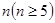 ,数列
,数列 :
: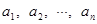 是1,2,…,
是1,2,…,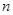 的一个排列,定义E(
的一个排列,定义E(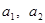 ,…,
,…,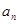 )
)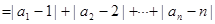 为数列
为数列 :
: ,
,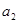 ,…,
,…,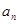 的位差和.
的位差和.
(1)当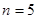 时,求数列
时,求数列 :1,3,4,2,5的位差和;
:1,3,4,2,5的位差和;
(2)若位差和E( ,
,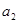 ,…,
,…,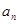 )=4,求满足条件的数列
)=4,求满足条件的数列 :
: ,
,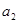 ,…,
,…,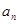 的个数;
的个数;
(3)若位差和 ,求满足条件的数列
,求满足条件的数列 :
: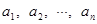 的个数.
的个数.
(本小题满分13分)已知定义在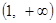 上的函数
上的函数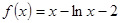 ,
,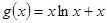 .
.
(1)求证: 存在唯一的零点,且零点属于(3,4);
存在唯一的零点,且零点属于(3,4);
(2)若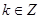 且
且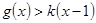 对任意的
对任意的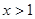 恒成立,求
恒成立,求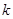 的最大值.
的最大值.
(本小题满分14分)如图,已知椭圆 的左焦点为F(
的左焦点为F( ,0),过点M(-3,0)作一条斜率大于0的直线
,0),过点M(-3,0)作一条斜率大于0的直线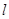 与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.
与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.
(1)求椭圆W的离心率;
(2)若∠MAC=60°,求直线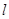 的斜率.
的斜率.
(本小题满分13分)设集合 ,从S的所有非空子集中,等可能地取出一个.
,从S的所有非空子集中,等可能地取出一个.
(1)设 ,若
,若 ,则
,则 ,就称子集A满足性质
,就称子集A满足性质 ,求所取出的非空子集满足性质
,求所取出的非空子集满足性质 的概率;
的概率;
(2)所取出的非空子集的最大元素为 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分13分)如图,四棱锥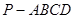 中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
(1)求三棱锥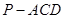 的外接球的体积;
的外接球的体积;
(2)求二面角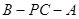 与二面角
与二面角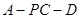 的正弦值之比.
的正弦值之比.