(本小题满分为12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 名学生。调査结果表明:在爱看课外书的
名学生。调査结果表明:在爱看课外书的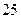 人中有
人中有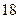 人作文水平好,另
人作文水平好,另 人作文水平一般;在不爱看课外书的
人作文水平一般;在不爱看课外书的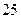 人中有
人中有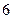 人作文水平好,另
人作文水平好,另 人作文水平一般.
人作文水平一般.
(Ⅰ)试根据以上数据建立一个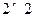 列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文
列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文 水平与爱看课外书有关系?
水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为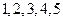 ,某
,某 名爱看
名爱看 课外书且作文水平一般的学生也分别编号为
课外书且作文水平一般的学生也分别编号为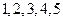 ,从这两组学生中各任选
,从这两组学生中各任选 人进行学习交流,求被选取的两名学生的编号之和为
人进行学习交流,求被选取的两名学生的编号之和为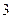 的倍数或
的倍数或 的倍数的概率.
的倍数的概率.
附: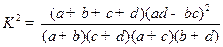
临界值表:
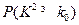 |
0. 10 |
0. 05 |
0. 025 |
0.010 |
0. 005 |
0. 001 |
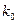 |
2. 706 |
3. 841 |
5. 024 |
6. 635 |
7. 879 |
10. 828 |
.△ABC的三个角A,B,C所对的边分别是a,b,c,向量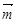 =(2,-1),
=(2,-1),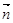 =(sinBsinC,
=(sinBsinC,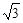 +2cosBcosC),且
+2cosBcosC),且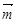 ⊥
⊥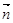 。⑴求角A的大小。⑵现给出以下三个条件:①B=45º;②2sinC-(
。⑴求角A的大小。⑵现给出以下三个条件:①B=45º;②2sinC-(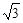
+1)sinB=0;③a=2。试从中再选择两个条件以确定△ABC,并求出所确定的△ABC的面积。
.将编号为1,2,3的三个小球随意放入编号为1,2,3的三个纸箱中,每个纸箱内有且只有一个小球,称此为一轮“放球”,设一轮“放球”后编号为i(i=1,2,3)的纸箱放入的小球编号为ai,定义吻合度误差为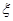 =|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足
=|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足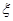 =2时的概率。⑵
=2时的概率。⑵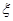 的数学期望。
的数学期望。
(本小题满分14分)
已知函数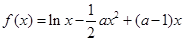 (
(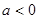 ).
).
(Ⅰ)求函数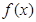 的单调区间;
的单调区间;
(Ⅱ)记函数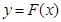 的图象为曲线
的图象为曲线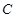 .设点
.设点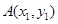 ,
,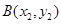 是曲线
是曲线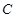 上的不同两点.
上的不同两点.
如果在曲线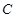 上存在点
上存在点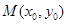 ,使得:①
,使得:① ;②曲线
;②曲线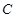 在点
在点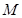 处的切线平行
处的切线平行
于直线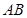 ,则称函数
,则称函数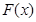 存在“中值相依切线”.试问:函数
存在“中值相依切线”.试问:函数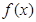 是否存在“中值相依切
是否存在“中值相依切
线”,请说明理由.
(本小题满分13分)
已知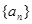 是单调递增的等差数列,首项
是单调递增的等差数列,首项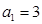 ,前
,前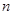 项和为
项和为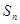 ,数列
,数列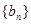 是等比数列,首项
是等比数列,首项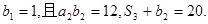 (Ⅰ)求
(Ⅰ)求 的通项公式。
的通项公式。
(Ⅱ)令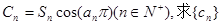 的前n项和
的前n项和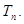
(本小题满分12分)已知椭圆的焦点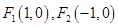 ,过
,过 作垂直于
作垂直于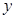 轴的直线被椭圆所截线段长为
轴的直线被椭圆所截线段长为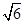 ,过
,过 作直线l与椭圆交于A、B两点.(I)求椭圆的标准方程;(Ⅱ)是否存在实数
作直线l与椭圆交于A、B两点.(I)求椭圆的标准方程;(Ⅱ)是否存在实数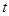 使
使 ,若存在,求
,若存在,求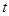 的值和直线
的值和直线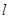 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.