哈尔滨市第六中学为绿化环境,移栽甲乙两种大树各 株,已知甲树种每株成活率为
株,已知甲树种每株成活率为 ,乙树种每株成活率为
,乙树种每株成活率为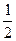 ,各株大树是否成活互不影响。求
,各株大树是否成活互不影响。求
(1)两种大 树各成活一株的概率;
树各成活一株的概率;
(2)设两种大树共成活的株数为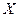 ,求
,求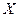 的分布列和期望;
的分布列和期望;
(3)设 表示“甲乙两种大树成活株数之和等于
表示“甲乙两种大树成活株数之和等于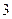 ”这一事件,用
”这一事件,用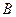 表示“甲成活的株数大于乙成活的株数”这一事件,求
表示“甲成活的株数大于乙成活的株数”这一事件,求 。
。
一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(1)从中同时摸出两个球,求两球颜色恰好相同的概率;
(2)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
已知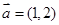 ,
,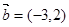 ,当
,当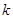 为何值时,
为何值时,
(1) 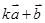 与
与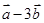 垂直?(2)
垂直?(2) 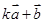 与
与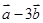 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
已知圆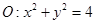 和圆
和圆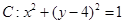 .
.
(1)判断圆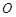 和圆
和圆 的位置关系;
的位置关系;
(2)过圆 的圆心
的圆心 作圆
作圆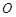 的切线
的切线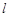 ,求切线
,求切线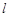 的方程;
的方程;
(3)过圆 的圆心
的圆心 作动直线
作动直线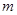 交圆
交圆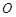 于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆
于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆 ,使得圆
,使得圆 经过点
经过点 ?若存在,求出圆
?若存在,求出圆 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
设数列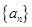 的前
的前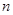 项和
项和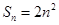 ,
,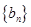 为等比数列,且
为等比数列,且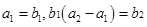 .
.
(1)求数列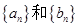 的通项公式;(2)设
的通项公式;(2)设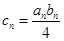 ,求数列
,求数列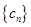 前
前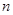 项和
项和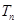 .
.
如图,在正方体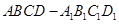 中,
中,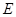 是
是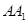 的中点.
的中点.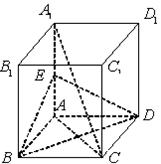
(1)求证: 平面
平面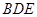 ;
;
(2)求证:平面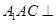 平面
平面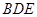 ;
;
(3)求直线BE与平面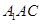 所成角的正弦值.
所成角的正弦值.