已知椭圆E:+=1(a>b>0),以F1(-c,0)为圆心,以a-c为半径作圆F1,过点B2(0,b)作圆F1的两条切线,设切点为M、N.
(1)若过两个切点M、N的直线恰好经过点B1(0,-b)时,求此椭圆的离心率;
(2)若直线MN的斜率为-1,且原点到直线MN的距离为4(-1),求此时的椭圆方程;
(3)是否存在椭圆E,使得直线MN的斜率k在区内取值?若存在,求出椭圆E的离心率e的取值范围;若不存在,请说明理由.
某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格.
(Ⅰ)估计所有参加笔试的1000名同学中,有面试资格的人数;
(Ⅱ)已知某中学有甲、乙两位同学取得面试资格,且甲的笔试比乙的高;面试时,要求每人回答两个问题,假设甲、乙两人对每一个问题答对的概率均为 ;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
如图, 平面
平面 凸多面体
凸多面体 的体积为
的体积为 ,
, 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面
 平面
平面 .
. 
已知点 是函数
是函数 的图象上一点,数列
的图象上一点,数列 的前n项和
的前n项和 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)将数列 前2013项中的第3项,第6项, ,第3k项删去,求数列
前2013项中的第3项,第6项, ,第3k项删去,求数列 前2013项中剩余项的和.
前2013项中剩余项的和.
已知 函数
函数 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 在区间
在区间 上的值域.
上的值域.
已知函数 .
.
(Ⅰ)求函数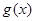 的极大值.
的极大值.
(Ⅱ)求证:存在 ,使
,使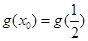 ;
;
(Ⅲ)对于函数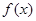 与
与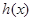 定义域内的任意实数x,若存在常数k,b,使得
定义域内的任意实数x,若存在常数k,b,使得 和
和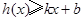 都成立,则称直线
都成立,则称直线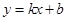 为函数
为函数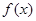 与
与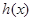 的分界线.试探究函数
的分界线.试探究函数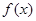 与
与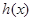 是否存在“分界线”?若存在,请给予证明,并求出k,b的值;若不存在,请说明理由.
是否存在“分界线”?若存在,请给予证明,并求出k,b的值;若不存在,请说明理由.