某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格.
(Ⅰ)估计所有参加笔试的1000名同学中,有面试资格的人数;
(Ⅱ)已知某中学有甲、乙两位同学取得面试资格,且甲的笔试比乙的高;面试时,要求每人回答两个问题,假设甲、乙两人对每一个问题答对的概率均为 ;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
(本小题满分10分)
已知向量 ,
, .
.
(1)设 ,求
,求 ;(2)若
;(2)若 ,求
,求 的值.
的值.
(附加题,本小题满分10分,该题计入总分)
已知数列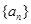 中,
中,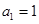 ,
,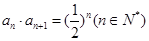 ,记
,记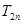 为
为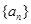 的前
的前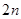 项的和.设
项的和.设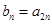 ,
,
(1)证明:数列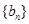 是等比数列;
是等比数列;
(2)不等式: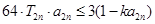 对于一切
对于一切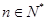 恒成立,求实数
恒成立,求实数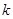 的最大值.
的最大值.
(本小题满分12分)
如图,已知斜三棱柱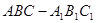 的侧面
的侧面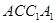 与底面ABC垂直,
与底面ABC垂直,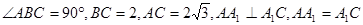
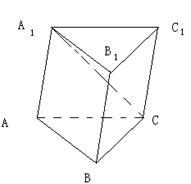
(1)求侧棱 与底面ABC所成的角;
与底面ABC所成的角;
(2)求侧面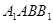 与底面ABC所成的角;
与底面ABC所成的角;
(3)求顶点C到平面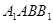 的距离.
的距离.
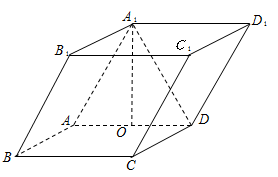
(本小题满分12分)如图,在四棱柱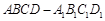 中,底面
中,底面 是矩形,且
是矩形,且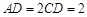 ,
, ,
,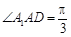 .若
.若 为
为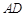 的中点,且
的中点,且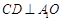 .
.
(1)求证: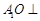 平面
平面 ;
;
(2)线段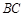 上是否存在一点
上是否存在一点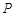 ,使得二面角
,使得二面角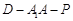 为
为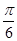 ?若存在,求出
?若存在,求出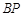 的长;不存在,说明理由.
的长;不存在,说明理由.
(本小题满分12分)
设数列 是公比小于1的正项等比数列,
是公比小于1的正项等比数列,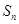 为数列
为数列 的前
的前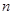 项和,已知
项和,已知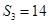 ,且
,且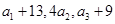 成等差数列。
成等差数列。
(1)求数列{an}的通项公式;
(2)若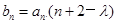 ,且数列
,且数列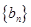 是单调递减数列,求实数
是单调递减数列,求实数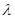 的取值范围。
的取值范围。