如右图所示，一张平行四边形的硬纸片ABC0D中，AD＝BD＝1，AB＝.沿它的对角线BD把△BDC0折起，使点C0到达平面ABC0D外点C的位置．
(1)证明：平面ABC0D⊥平面CBC0；
(2)如果△ABC为等腰三角形，求二面角A－BD－C的大小
设F1、F2分别为椭圆C：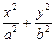
=1（a＞b＞0）的左、右两个焦点.
（1）若椭圆C上的点A（1，
）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标；
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程；
已知圆C在x轴上的截距为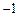
和3，在y轴上的一个截距为1．
（1）求圆C的标准方程；
（2）若过点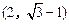
的直线l被圆C截得的弦AB的长为4，求直线l的倾斜角．
已知圆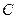
与两坐标轴都相切，圆心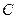到直线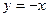
的距离等于
。
（1）求圆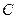的方程。
（2）若直线
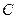与圆相切，求证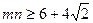
。
设F1、F2分别为椭圆C：
=1（a＞b＞0）的左、右两个焦点.
（1）若椭圆C上的点A（1，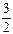
）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标；
（2）设点P是（1）中所得椭圆上的动点，当P在何位置时，
最大，说明理由，并求出最大值。
设向量
，点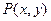
为动点，已知
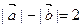，且点P的轨迹C1。若抛物线C2的顶点在原点，与轨迹C1共焦点F，设抛物线C2与轨迹C1的交点分别为M、N。
（1）分虽求轨迹为C1与抛物线C2的方程；
（2）过F作一条与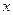
轴不垂直的直线，与曲线C1在点M、N左侧的部分交于C、D两点，与曲线C2在点M、N左侧的部分交于B、E两点，若G为CD的中点，H为BE的中点，问
是否为定值？若是，求出定值；若不是，请说明理由。