【2015高考福建,文21】已知函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位长度,再向下平移
个单位长度,再向下平移 (
( )个单位长度后得到函数
)个单位长度后得到函数 的图象,且函数
的图象,且函数 的最大值为2.
的最大值为2.
(ⅰ)求函数 的解析式;
的解析式;
(ⅱ)证明:存在无穷多个互不相同的正整数 ,使得
,使得 .
.
在△ABC中,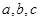 分别是角A,B,C的对边,
分别是角A,B,C的对边,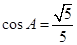 ,
,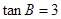 .
.
(1)求角 的值;
的值;
(2)若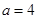 ,求△ABC面积.
,求△ABC面积.
如图, 在直三棱柱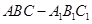 中,
中,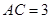 ,
,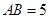 ,
,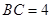 ,点
,点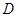 是
是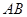 的中点,
的中点,
⑴ 求证: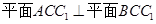 ;
;
⑵ 求证:
(本小题满分14分)
已知函数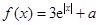 (
( …是自然对数的底数)的最小值为
…是自然对数的底数)的最小值为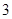 .
.
(Ⅰ)求实数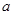 的值;
的值;
(Ⅱ)已知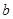
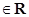 且
且 ,试解关于
,试解关于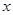 的不等式
的不等式 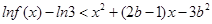 ;
;
(Ⅲ)已知 且
且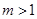 .若存在实数
.若存在实数 ,使得对任意的
,使得对任意的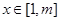 ,都有
,都有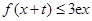 ,试求
,试求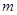 的最大值.
的最大值.
(本小题满分12分)
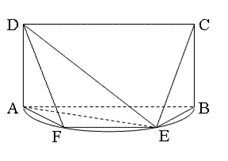
如图,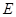 是以
是以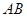 为直径的半圆上异于
为直径的半圆上异于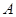 、
、 的点,矩形
的点,矩形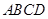 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且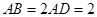 .
.
(Ⅰ)求证: ;
;
(Ⅱ)设平面 与半圆弧的另一个交点为
与半圆弧的另一个交点为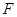 .
.
①试证: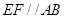 ;
;
②若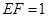 ,求三棱锥
,求三棱锥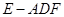 的体积.
的体积.
(本小题满分12分)
已知 为坐标原点,对于函数
为坐标原点,对于函数 ,称向量
,称向量 为函数
为函数 的伴随向量,同时称函数
的伴随向量,同时称函数 为向量
为向量 的伴随函数.
的伴随函数.
(Ⅰ)设函数 ,试求
,试求 的伴随向量
的伴随向量 的模;
的模;
(Ⅱ)记 的伴随函数为
的伴随函数为 ,求使得关于
,求使得关于 的方程
的方程 在
在 内恒有两个不相等实数解的实数
内恒有两个不相等实数解的实数 的取值范围.
的取值范围.