某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为[80,90)、[90,100)、[100,110)、[110,120)、[120,130),由此得到两个班测试成绩的频率分布直方图: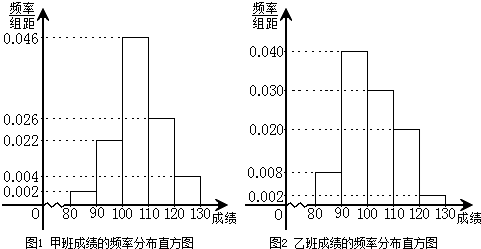
(Ⅰ)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
| |
成绩小于100分 |
成绩不小于100分 |
合计 |
| 甲班 |
a= _________ |
b= _________ |
50 |
| 乙班 |
c=24 |
d=26 |
50 |
| 合计 |
e= _________ |
f= _________ |
100 |
(Ⅱ)现从乙班50人中任意抽取3人,记ξ表示抽到测试成绩在[100,120)的人数,求ξ的分布列和数学期望Eξ.
附:K2= ,其中n=a+b+c+d
,其中n=a+b+c+d
| P(K2≥k0) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
2.072 |
2.706 |
3.841 |
5.204 |
6.635 |
7.879 |
10.828 |
(本小题满分12分)在三棱柱 中,侧面
中,侧面 为矩形,
为矩形, ,
, ,
, 为
为 的中点,
的中点, 与
与 交于点
交于点 ,
, 侧面
侧面 .
.
(1)证明: ;
;
(2)若 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)为迎接2014年“马”年的到来,某校举办猜奖活动,参与者需先后回答两道选择题,问题 有三个选项,问题
有三个选项,问题 有四个选项,但都只有一个选项是正确的,正确回答问题
有四个选项,但都只有一个选项是正确的,正确回答问题 可获奖金
可获奖金 元,正确回答问题
元,正确回答问题 可获奖金
可获奖金 元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
(1)如果参与者先回答问题 ,求其恰好获得奖金
,求其恰好获得奖金 元的概率;
元的概率;
(2)试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
(本小题满分12分)如图 中,已知点
中,已知点 在
在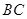 边上,满足
边上,满足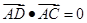 ,
, ,
, ,
,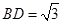 .
.
(1)求 的长;
的长;
(2)求 .
.
设函数

(1)若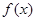 的最小值为3,求
的最小值为3,求 的值;
的值;
(2)求不等式 的解集.
的解集.
已知曲线 (
( 为参数),
为参数), (
( 为参数).
为参数).
(1)化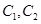 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)过曲线 的左顶点且倾斜角为
的左顶点且倾斜角为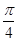 的直线
的直线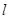 交曲线
交曲线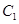 于
于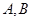 两点,求
两点,求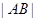 .
.