(本小题满分12分)为迎接2014年“马”年的到来,某校举办猜奖活动,参与者需先后回答两道选择题,问题 有三个选项,问题
有三个选项,问题 有四个选项,但都只有一个选项是正确的,正确回答问题
有四个选项,但都只有一个选项是正确的,正确回答问题 可获奖金
可获奖金 元,正确回答问题
元,正确回答问题 可获奖金
可获奖金 元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
(1)如果参与者先回答问题 ,求其恰好获得奖金
,求其恰好获得奖金 元的概率;
元的概率;
(2)试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
已知动点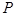 到点
到点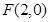 的距离比它到直线
的距离比它到直线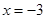 的距离小1,记点
的距离小1,记点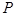 的轨迹为
的轨迹为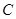 .
.
(1)求曲线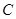 的方程;
的方程;
(2)过点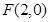 的直线
的直线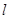 交曲线
交曲线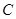 于
于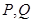 两点,若
两点,若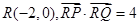 ,求直线
,求直线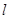 的方程
的方程
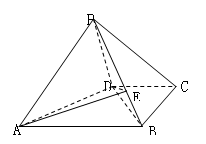
如图,在四棱锥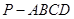 中,底面
中,底面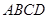 是直角梯形,
是直角梯形,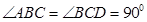 ,面
,面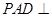 面
面 ,
,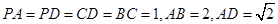
(1)证明: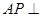 面
面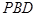 ;
;
(2)若点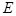 是线段
是线段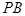 上一点,且
上一点,且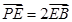 ,求三棱锥
,求三棱锥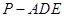 的体积。
的体积。
如图,在四面体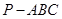 中,
中,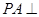 平面
平面 ,
,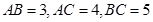 ,且
,且 、
、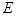 、
、 、
、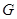 分别为
分别为 、
、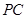 、
、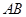 、
、 的中点.
的中点.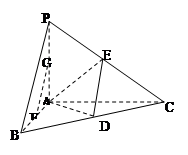
(1)证明: ∥平面
∥平面 ;
;
(2)若直线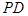 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为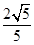 ,求
,求 的长。
的长。
已知两条直线 的交点为
的交点为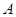 ,动直线
,动直线
(1)若直线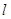 过点
过点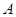 ,求实数
,求实数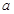 的值;
的值;
(2)若直线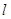 与
与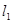 垂直,求三条直线
垂直,求三条直线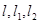 围成三角形的面积。
围成三角形的面积。
已知椭圆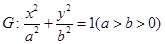 的离心率为
的离心率为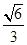 ,右焦点为(
,右焦点为(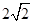 ,0),斜率为1的直线
,0),斜率为1的直线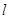 与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
(Ⅰ)求椭圆G的方程;
(Ⅱ)求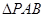 的面积.
的面积.