(本小题满分14分)
已知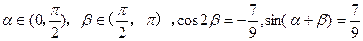 .
.
(Ⅰ)求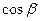 的值;
的值;
(Ⅱ)求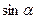 的值.
的值.
(本小题满分14分)已知:对于数列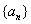 ,定义
,定义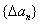 为数列
为数列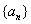 的一阶差分数列,其中
的一阶差分数列,其中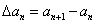 , (1)若数列
, (1)若数列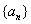 的通项公式
的通项公式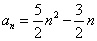 (
(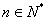 ),求:数列
),求:数列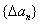 的通项公式; (2)若数列
的通项公式; (2)若数列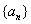 的首项是1,且满足
的首项是1,且满足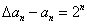 ,
,
①设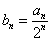 ,求证:数列
,求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
②求:数列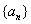 的通项公式及前
的通项公式及前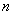 项和
项和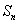
(本小题满分13分)已知:向量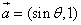 ,向量
,向量 ,
, ,
,
(1)若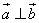 ,求:
,求: 的值; (2)求:
的值; (2)求: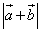 的最大值。
的最大值。
(本小题满分13分)已知:定义在R上的函数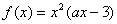 ,其中a为常数。
,其中a为常数。
(1)若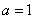 ,求:
,求: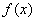 的图象在点
的图象在点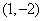 处的切线方程;
处的切线方程;
(2)若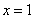 是函数
是函数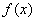 的一个极值点,求:实数a的值;
的一个极值点,求:实数a的值;
(3)若函数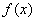 在区间
在区间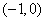 上是增函数,求:实数a的取值范围。
上是增函数,求:实数a的取值范围。
(本小题满分13分)已知:若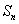 是公差不为0的等差数列
是公差不为0的等差数列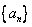 的前
的前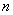 项和,且
项和,且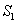 、
、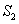 、
、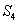 成等比数列。 (1)求:数列
成等比数列。 (1)求:数列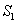 、
、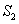 、
、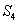 的公比; (2)若
的公比; (2)若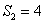 ,求:数列
,求:数列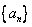 的通项公式。
的通项公式。