如图,在四面体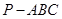 中,
中,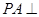 平面
平面 ,
,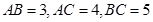 ,且
,且 、
、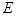 、
、 、
、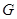 分别为
分别为 、
、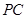 、
、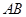 、
、 的中点.
的中点.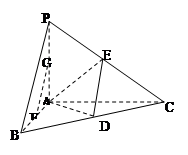
(1)证明: ∥平面
∥平面 ;
;
(2)若直线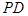 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为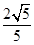 ,求
,求 的长。
的长。
(本小题满分13分)
在一个月内分批购入每张价值为20元的书桌共36台,每批都购入x台(x是正整数), 且每批均需付运费4元,储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比,若每批购入4台,则该月需用去运费和保管费共52元,现在全月只有48元资金可以用于支付运费和保管费.
且每批均需付运费4元,储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比,若每批购入4台,则该月需用去运费和保管费共52元,现在全月只有48元资金可以用于支付运费和保管费.
(1)求该月需用去的运费和保管费的总费用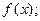
(2)能否恰当地安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
(本题12分)等比数列 中,已知
中,已知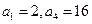


(I)求数列 的通项公式;
的通项公式;
(Ⅱ)若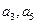 分别为等差数列
分别为等差数列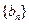 的第3项和第5项,试求数列
的第3项和第5项,试求数列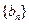 的通项公式及前
的通项公式及前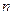 项和
项和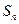 。
。
(本小题满分12分)已知向量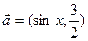 ,
, .
.
(1)当 ∥
∥ 时,求
时,求 的值;
的值;
(2)求 在
在 上的值域.
上的值域.
(本小题满分12分)已知不等式 的解集为
的解集为 .
.
(1)求 ;
;
(2)解不等式
(本小题满分13分)已知曲线 ,从
,从 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,再从点
,再从点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,设
,设
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)记 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: ;
;
(3)若已知 ,记数列
,记数列 的前
的前 项和为
项和为 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小.
的大小.