设函数f(x)=ax3+bx2+c,其中a+b=0,a,b,c均为常数,曲线y=f(x)在(1,f(1))处的切线方程为x+y﹣1=0.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调区间.
(本小题满分12分)
已知矩形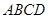 与正三角形
与正三角形 所在的平面互相垂直,
所在的平面互相垂直, 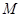 、
、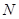 分别为棱
分别为棱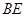 、
、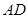 的中点,
的中点,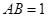 ,
,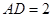 ,
,
(1)证明:直线 平面
平面 ;
;
(2)求二面角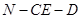 的大小.
的大小.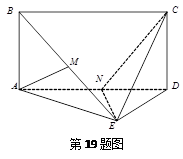
(本小题共12分)
甲,乙两人进行乒乓球比赛,约定每局胜者得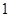 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多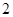 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为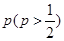 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
.
(Ⅰ)求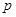 的值;
的值;
(Ⅱ)设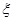 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量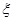 的分布列和数学期望
的分布列和数学期望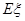 .
.
(文)(本小题14分)已知函数 (
( 为实数).
为实数).
(1)当 时, 求
时, 求 的最小值;
的最小值;
(2)若 在
在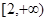 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围.
(理) 已知 ,其中
,其中 是自然常数,
是自然常数, [
[
(1)讨论 时,
时,  的单调性、极值;
的单调性、极值;
(2)求证:在(Ⅰ)的条件下, ;
;
(3)是否存在实数 ,使
,使 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知椭圆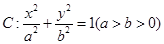 的离心率
的离心率 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足 (1)求椭圆C的方程;
(1)求椭圆C的方程;
(2)是否存在直线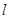 ,当直线
,当直线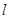 交椭圆于P、Q两点时,使点F恰为
交椭圆于P、Q两点时,使点F恰为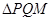 的垂心(三角形三条高的交点)?若存在,求出直线
的垂心(三角形三条高的交点)?若存在,求出直线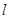 方程;若不存在,请说明理由。
方程;若不存在,请说明理由。