【2015高考湖北,文18】某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
 |
0 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
 |
0 |
5 |
|
 |
0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数 的解析式;
的解析式;
(Ⅱ)将 图象上所有点向左平行移动
图象上所有点向左平行移动 个单位长度,得到
个单位长度,得到 图象,求
图象,求 的图象离原点
的图象离原点 最近的对称中心.
最近的对称中心.
(本小题满分12分)
设{an}是等差数列,{bn}是各项为正项的等比数列,且a1=b1="1," a3+b5="21," a5+b3=13.
(1)求{an}, {bn}的通项公式;
(2)求数列{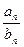 }的前n项和Sn;
}的前n项和Sn;
(本小题满分12分)
已知向量 =(sin
=(sin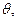 1),
1),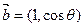 ,
, .
.
(1)若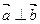 ,求
,求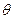 ;
;
(2)求| 的最
的最 大值。
大值。
选修4-5:不等式选讲
设函数 .
.
(1)解不等式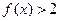 ;
;
(2)求函数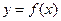 的最小值.
的最小值.
一条直线经过点P(3,2),并且分别满足下列条件,求直线方程:
(1)倾斜角是直线x-4y+3=0的倾斜角的2倍;
(2)与x、y轴的正半轴交于A、B两点,且△AOB的面积最小(O为坐标原点).
如图,矩形 的两条对角线相交于点
的两条对角线相交于点 ,
,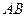 边所在直线的方程为
边所在直线的方程为 , 点
, 点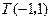 在
在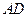 边所在直线上.
边所在直线上.
(I)求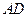 边所在直线的方程;
边所在直线的方程;
(II)求矩形 外接圆的方程;
外接圆的方程;