某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为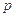 ,
,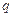 (
(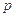 >
>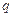 ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
| ξ |
0 |
1 |
2 |
3 |
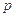 |
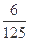 |
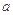 |
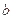 |
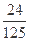 |
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求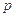 ,
,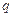 的值;
的值;
(Ⅲ)求数学期望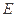 ξ。
ξ。
对于数列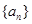 ,把
,把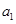 作为新数列
作为新数列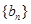 的第一项,把
的第一项,把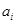 或
或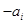 (
(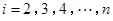 )作为新数列
)作为新数列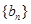 的第
的第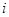 项,数列
项,数列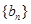 称为数列
称为数列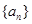 的一个生成数列.例如,数列
的一个生成数列.例如,数列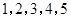 的一个生成数列是
的一个生成数列是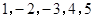 .已知数列
.已知数列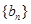 为数列
为数列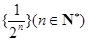 的生成数列,
的生成数列,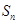 为数列
为数列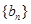 的前
的前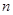 项和.
项和.
(1)写出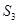 的所有可能值;
的所有可能值;
(2)若生成数列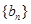 满足
满足 ,求数列
,求数列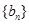 的通项公式;
的通项公式;
(3)证明:对于给定的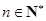 ,
,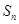 的所有可能值组成的集合为
的所有可能值组成的集合为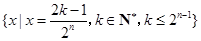 .
.
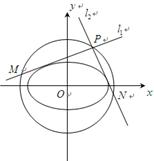
给定椭圆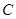 :
: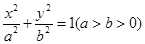 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆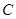 的“准圆”.若椭圆
的“准圆”.若椭圆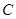 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到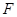 的距离为
的距离为 .
.
(1)求椭圆 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点 是椭圆
是椭圆 的“准圆”上的动点,过点
的“准圆”上的动点,过点 作椭圆的切线
作椭圆的切线 交“准圆”于点
交“准圆”于点 .
.
(ⅰ)当点 为“准圆”与
为“准圆”与 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 的方程,
的方程,
并证明 ;
;
(ⅱ)求证:线段 的长为定值.
的长为定值.
设函数 .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若函数 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(3)过坐标原点 作曲线
作曲线 的切线,证明:切点的横坐标为
的切线,证明:切点的横坐标为 .
.
如图,正三棱柱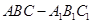 的底面边长是
的底面边长是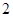 ,侧棱长是
,侧棱长是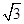 ,
,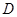 是
是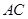 的中点.
的中点.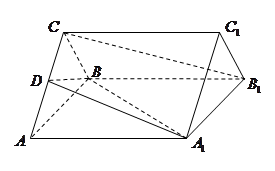
(1)求证: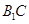 ∥平面
∥平面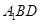 ;
;
(2)求二面角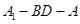 的大小;
的大小;
(3)在线段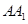 上是否存在一点
上是否存在一点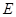 ,使得平面
,使得平面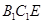
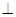 平面
平面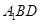 ,若存在,求出
,若存在,求出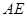 的长;若不存在,说明理由.
的长;若不存在,说明理由.
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
罗非鱼的汞含量(ppm)
 |
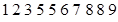 |
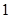 |
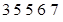 |
《中华人民共和国环境保护法》规定食品的汞含量不得超过 ppm.
ppm.
(1)检查人员从这 条鱼中,随机抽出
条鱼中,随机抽出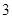 条,求
条,求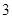 条中恰有
条中恰有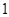 条汞含量超标的概率;
条汞含量超标的概率;
(2)若从这批数量很大的鱼中任选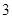 条鱼,记
条鱼,记 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此 条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求 的分布列及数学期望
的分布列及数学期望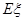 .
.