某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是,每次测试时间间隔恰当,每次测试通过与否互相独立.
(1)求该学生考上大学的概率;
(2)求该学生经过4次测试考上大学的概率
已知函数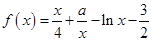 ,其中
,其中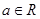 ,且曲线
,且曲线 在点
在点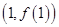 处的切线垂直于直线
处的切线垂直于直线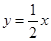
(Ⅰ)求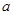 的值;
的值;
(Ⅱ)求函数 的单调区间及极值.
的单调区间及极值.
已知函数
(Ⅰ)求函数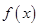 的最大值及此时
的最大值及此时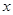 的值;
的值;
(Ⅱ)在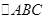 中,
中,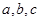 分别为内角
分别为内角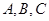 所对的边,若
所对的边,若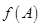 为
为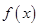 的最大值,且
的最大值,且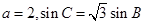 ,求
,求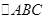 的面积.
的面积.
已知等比数列 的前
的前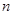 项和为
项和为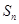 ,
,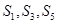 成等差数列,且
成等差数列,且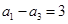
(Ⅰ)求 的通项公式
的通项公式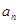 ;
;
(Ⅱ)求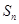 ,并求满足
,并求满足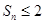 的
的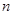 值.
值.
已知函数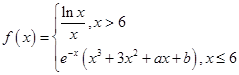 ,其中
,其中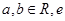 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当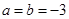 时,求函数
时,求函数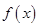 的单调区间;
的单调区间;
(Ⅱ)当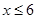 时,若函数
时,若函数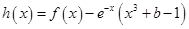 存在两个相距大于2的极值点,求实数
存在两个相距大于2的极值点,求实数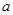 的取值范围;
的取值范围;
(Ⅲ)若函数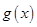 与函数
与函数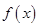 的图象关于
的图象关于 轴对称,且函数
轴对称,且函数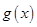 在
在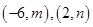 单调递减,在
单调递减,在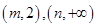 单调递增,试证明:
单调递增,试证明: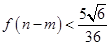 .
.
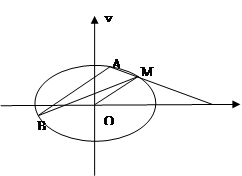
如图,已知椭圆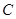 的中心在原点,其一个焦点与抛物线
的中心在原点,其一个焦点与抛物线 的焦点相同,又椭圆
的焦点相同,又椭圆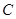 上有一点
上有一点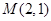 ,直线
,直线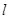 平行于
平行于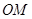 且与椭圆
且与椭圆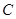 交于
交于 两点,连
两点,连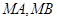
(Ⅰ)求椭圆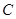 的方程;
的方程;
(Ⅱ)当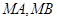 与
与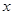 轴所构成的三角形是以
轴所构成的三角形是以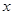 轴上所在线段为底边的等腰三角形时,求直线
轴上所在线段为底边的等腰三角形时,求直线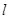 在
在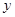 轴上截距的取值范围.
轴上截距的取值范围.