（本小题满分12分）
在
中，内角
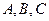所对边长分别为
，
，
，
.
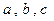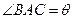（1）求
的最大值及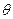
的取值范围；
（2）求
函数
的最值.
在对人们休闲的一次调查中，共调查了124人，其中女性70人，男性54人。女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动。
（1）根据以上数据建立一个
的列联表；
| P(k2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.83 |
（2）检验性别与休闲方式是否有关系。（本题可以参考两个分类变量x和y有关系的可信度表:）
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
用三段论证明函数
在（－∞，+∞）上是增函数.
用分析法证明：
已知
且
，当
时，恒有
求
的解析式；
若
的解集为空集，求
的范围。
已知曲线
：
,数列
的首项
，且
当
时，点
恒在曲线上，数列{
}满足
(1)试判断数列
是否是等差数列？并说明理由；
(2)求数列和的通项公式；
(3)设数列
满足
，试比较数列的前
项和
与
的大小．