(本小题满分14分)
已知 是抛物线
是抛物线
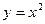 上两动点,直线
上两动点,直线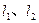 分别是抛物线
分别是抛物线 在点
在点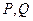 处的切线,且
处的切线,且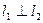 ,
, .
.
( 1)求点
1)求点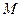 的纵坐标;
的纵坐标;
(2)直线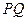 是否经过一定点
是否经过一定点 ?试证之;
?试证之;
(3)求 的面积的最小值
的面积的最小值
已知函数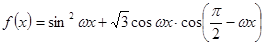 ,
,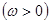 且函数
且函数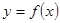 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为
(Ⅰ)求 的值;
的值; (Ⅱ)若函数
(Ⅱ)若函数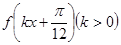 在区间
在区间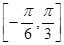 上单调递增,求k的取值范围.
上单调递增,求k的取值范围.
某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
| 时间 |
第4天 |
第32天 |
第60天 |
第90天 |
| 价格(千元) |
23 |
30 |
22 |
7 |
(1)、写出价格 关于时间
关于时间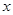 的函数关系式(
的函数关系式(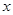 表示投放市场的第
表示投放市场的第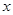 天)
天)
(2)、销售量 与时间
与时间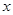 的函数关系为:
的函数关系为: ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
已知向量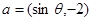 与
与 互相垂直,其中
互相垂直,其中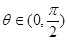
(1)求 和
和 的值
的值
(2)若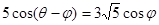 ,
,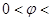
 ,求
,求 的值
的值
已知集合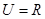 ,
,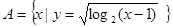 ,
,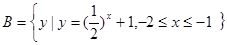 ,
,
(1)求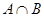 ;(2)若
;(2)若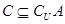 ,求实数
,求实数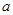 的取值范围.
的取值范围.
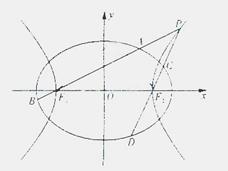
如图,已知椭圆 的离心率为
的离心率为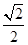 ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为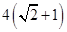 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程
(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1
(Ⅲ)是否存在常数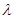 ,使得|AB|+|CD|=
,使得|AB|+|CD|=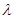 |AB|·|CD|恒成立?若存在,求
|AB|·|CD|恒成立?若存在,求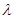 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。