已知函数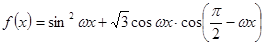 ,
,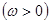 且函数
且函数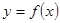 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为
(Ⅰ)求 的值;
的值; (Ⅱ)若函数
(Ⅱ)若函数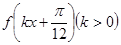 在区间
在区间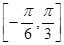 上单调递增,求k的取值范围.
上单调递增,求k的取值范围.
(本小题满分14分)
二次函数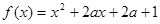 .
.
(1)若对任意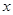
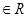 有
有 恒成立,求实数
恒成立,求实数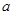 的取值范围;
的取值范围;
(2)讨论函数 在区间
在区间 上的单调性;
上的单调性;
(3)若对任意的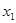 ,
,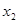
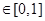 有
有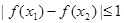 恒成立,求实数
恒成立,求实数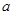 的取值范围.
的取值范围.
已知椭圆 过点
过点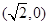 ,且离心率为
,且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2) 为椭圆
为椭圆 的左右顶点,点
的左右顶点,点 是椭圆
是椭圆 上异于
上异于 的动点,直线
的动点,直线 分别交直线
分别交直线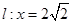 于
于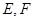 两点.
两点.
证明:以线段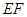 为直径的圆恒过
为直径的圆恒过 轴上的定点.
轴上的定点.
(本小题满分14分)
执行下面框图(图3)所描述的算法程序,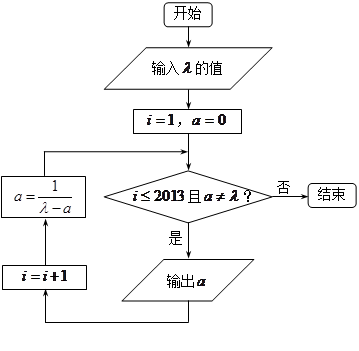
记输出的一列数依次为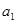 ,
,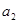 ,…,
,…,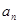 ,
, ,
,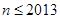 .
.
(注:框图中的赋值符号“ ”也可以写成“
”也可以写成“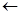 ”或“:
”或“: ”)
”)
(1)若输入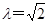 ,直接写出输出结果;
,直接写出输出结果;
(2)若输入 ,证明数列
,证明数列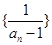 是等差数列,并求出数列
是等差数列,并求出数列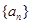 的通项公式.
的通项公式.
(本小题满分14分)
如图所示,四棱锥 中,底面
中,底面 为正方形,
为正方形,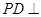 平面
平面 ,
,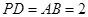 ,
,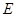 ,
, ,
,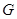 分别为
分别为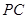 、
、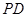 、
、 的中点.
的中点.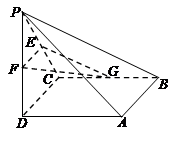
(1)求证: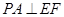 ;
;
(2)求平面EFG与平面ABCD所成锐二面角的余弦值.
(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):
 男女
男女 15 7 7 8 9 9 9
15 7 7 8 9 9 9
9 816 0 0 1 2 4 5 8 9
8 6 5 017 2 5 6
7 4 2 118 0
1 019
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?