(本小题满分16分)已知函数f(x)=ax2-(2a+1)x+2lnx(a为正数).
(1) 若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2) 求f(x)的单调区间;
(3) 设g(x)=x2-2x,若对任意的x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求实数a的取值范围.
如图,已知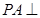 ⊙
⊙ 所在的平面,AB是⊙
所在的平面,AB是⊙ 的直径,
的直径,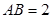 ,
,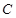 是⊙
是⊙ 上一点,且
上一点,且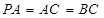 ,
,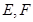 分别为
分别为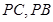 中点。
中点。
(Ⅰ)求证: 平面
平面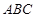 ;
;
(Ⅱ)求证: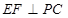 ;
;
(Ⅲ)求三棱锥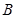 -
-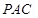 的体积。
的体积。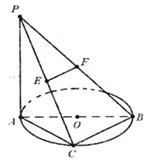
已知圆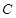 经过两点
经过两点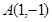 和
和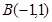 ,且圆心在直线
,且圆心在直线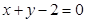 上。
上。
(Ⅰ)求圆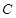 的方程;
的方程;
(Ⅱ)若以圆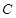 为底面的等边圆锥(轴截面为正三角形),求其内接正方体的棱长。
为底面的等边圆锥(轴截面为正三角形),求其内接正方体的棱长。
已知椭圆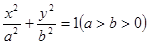 的右焦点为
的右焦点为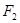 (3,0),离心率为
(3,0),离心率为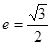 。
。
(1)求椭圆的方程。
(2)设直线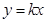 与椭圆相交于A,B两点,M,N分别为线段
与椭圆相交于A,B两点,M,N分别为线段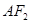 ,
,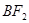 的中点,若坐标原点O在以MN为直径的圆上,求
的中点,若坐标原点O在以MN为直径的圆上,求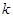 的值。
的值。
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点。
(1)证明:EF∥平面PAD;
(2)求三棱锥E-ABC的体积V。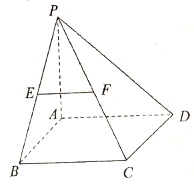
已知Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-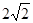 ),顶点C在
),顶点C在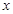 轴上。
轴上。
(1)求BC边所在直线的方程;
(2)圆M为Rt△ABC外接圆,其中M为圆心,求圆M的方程;
(3)直线 与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面积最小时的切线方程。
与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面积最小时的切线方程。