已知Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-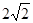 ),顶点C在
),顶点C在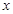 轴上。
轴上。
(1)求BC边所在直线的方程;
(2)圆M为Rt△ABC外接圆,其中M为圆心,求圆M的方程;
(3)直线 与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面积最小时的切线方程。
与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面积最小时的切线方程。
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图,根据统计图:
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?
(3)甲、乙两个网站哪个更受欢迎?并说明理由。 
某区高二年级的一次数学统考中,随机抽取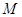 名同学的成绩,数据的分组统计表如下:
名同学的成绩,数据的分组统计表如下:
| 分组 |
频数 |
频率 |
频率/组距 |
| (40,50] |
2 |
0.02 |
0.002 |
| (50,60] |
4 |
0.04 |
0.004 |
| (60,70] |
11 |
0.11 |
0.011 |
| (70,80] |
38 |
0.38 |
0.038 |
| (80,90] |
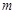 |
 |
 |
| (90,100] |
11 |
0.11 |
0.011 |
| 合计 |
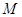 |
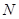 |
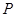 |
(1)求出表中 的值;
的值;
(2)若该区高二学生有5000人,试估计这次统考中该区高二学生的平均分数及分数在区间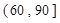 内的人数.
内的人数.
已知角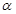 的终边上一点
的终边上一点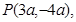
(1)当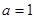 时,求
时,求 的值;
的值;
(2)当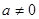 时,求
时,求 的值
的值
已知数列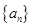 满足
满足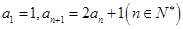
(Ⅰ)求数列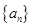 的通项公式;
的通项公式;
(Ⅱ)若数列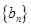 满足
满足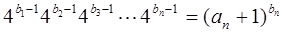 ,证明:
,证明: 是等差数列;
是等差数列;
(Ⅲ)证明: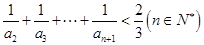
设G为 的重心,过G的直线
的重心,过G的直线 分别交AB,AC于
分别交AB,AC于 ,已知:
,已知: ,
, 和
和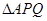 的面积分别为
的面积分别为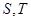 ,
,
(Ⅰ)求 的值; (Ⅱ) 求
的值; (Ⅱ) 求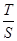 的取值范围.
的取值范围.