(本题满分15分)
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学纳法证明你的猜想,并求出an的表达式.
(本题满分15分)
已知a、b∈(0,+∞),且a+b=1,
求证:(1) ab≤ (2)
(2) +
+ ≥8; (3)
≥8; (3)  +
+  ≥
≥ . (5分+5分+5分)
. (5分+5分+5分)
(本小题满分14分)
已知 p:
p: ,q:
,q: .
.
⑴ 若p是q充分不必要条件,求实数 的取值范围;
的取值范围;
⑵若“非p”是“非q”的充分不必要条件,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知 为复数,
为复数, 和
和 均为实数,其中
均为实数,其中 是虚数单位.
是虚数单位.
(Ⅰ)求复数 ;
;
(Ⅱ)若复数 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数 的取值范围.
的取值范围.
((本小题满分12分)
如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=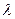 a(0<
a(0<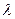 ≦1).
≦1).
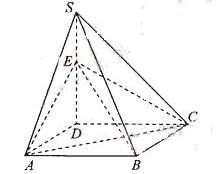
 (Ⅰ)求证:对任意的
(Ⅰ)求证:对任意的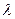
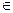 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求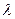 的值。
的值。