(.在一次购物抽奖活动中,假设某10张券中有一等奖奖券1张,可获价值50元的奖品;有二等奖奖券3张,每张可获价值10元的奖品;其余6张没奖。某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列。
在 平面上有一系列点
平面上有一系列点
 对每个自然数
对每个自然数 ,点
,点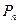 位于函数
位于函数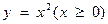 的图象上.以点
的图象上.以点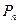 为圆心的⊙
为圆心的⊙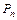 与
与 轴都相切,且⊙
轴都相切,且⊙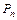 与⊙
与⊙ 又彼此外切.若
又彼此外切.若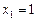 ,且
,且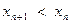
 .
.
(1)求证:数列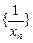 是等差数列;
是等差数列;
(2)设⊙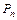 的面积为
的面积为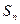 ,
,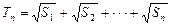 , 求证:
, 求证:
如图直角梯形OABC中, ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
(Ⅰ)求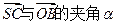 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(Ⅱ)设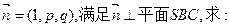
①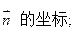
②OA与平面SBC的夹角 (用反三角函数表示);
(用反三角函数表示);
③O到平面SBC的距离.
(Ⅲ)设
① .
.
②异面直线SC、OB的距离为 .
(注:(Ⅲ)只要求写出答案).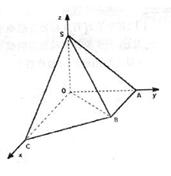
同时抛掷15枚均匀的硬币一次
(1)试求至多有1枚正面向上的概率;
(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?
请说明理由.
已知双曲线C的方程为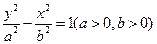 ,离心率
,离心率 ,
,
顶点到渐近线的距离为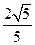 。 求 (1)双曲线C的方程;
。 求 (1)双曲线C的方程;
(2)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若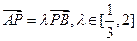 ,求
,求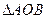 面积的取值范围。
面积的取值范围。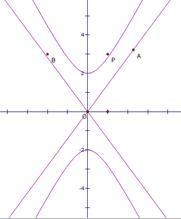
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(2)求这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.