本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知 的三个顶点在抛物线
的三个顶点在抛物线 :
: 上运动,
上运动,
(1). 求 的焦点坐标;
的焦点坐标;
(2). 若点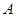 在坐标原点, 且
在坐标原点, 且 ,点
,点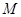 在
在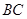 上,且
上,且  ,
,
求点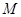 的轨迹方程;
的轨迹方程;
(3). 试研究: 是否存在一条边所在直线的斜率为 的正三角形
的正三角形 ,若存在,求出这个正三角形
,若存在,求出这个正三角形 的边长,若不存在,说明理由.
的边长,若不存在,说明理由.
(本小题满分l4分)已知函数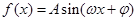 (其中
(其中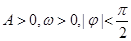 )的图象如下图所示。
)的图象如下图所示。
(1)求 ,
, 及
及 的值;
的值;
(2)若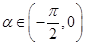 ,且
,且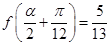 ,求
,求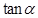 的值.。
的值.。
(本小题满分l2分)已知函数 。
。
(1)求函数 的最小正周期;
的最小正周期;
(2)若 ,且
,且 ,求
,求 的值。
的值。
(本小题12分)已知函数
(1)求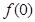 的值;
的值;
(2)求函数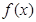 的最大值,并求
的最大值,并求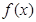 取最大值时
取最大值时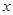 取值的集合;
取值的集合;
(3)求函数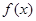 的单调增区间。
的单调增区间。
如图8所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的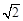 倍,点P在侧棱SD上,且
倍,点P在侧棱SD上,且 .
.
(Ⅰ)求证:AC⊥SD;
(Ⅱ)求二面角P-AC-D的大小;
(Ⅲ)侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.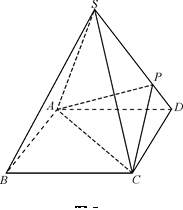
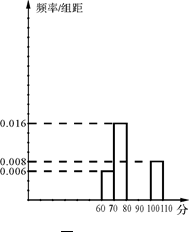
某班50名学生在一次数学考试中,成绩都属于区间[60,110],将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110],部分频率分布直方图如图7所示,及格(成绩不小于90分)的人数为20.
(Ⅰ)请补全频率分布直方图;
(Ⅱ)由此估计该班的平均分;
(Ⅲ)在成绩属于[60,70)∪[100,110]的学生中任取两人,成绩记为 ,求
,求 的概率.
的概率.