(本小题满分12分)
已知斜三棱柱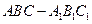 ,
,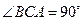 ,
,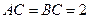 ,
,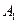 在底面
在底面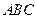 上的射影恰
上的射影恰
为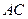 的中点
的中点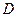 ,
,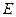 为
为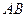 的中点,
的中点,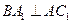 .
.
(I)求证: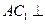 平面
平面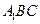 ;
;
(II)求二面角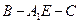 余弦值的大小.
余弦值的大小.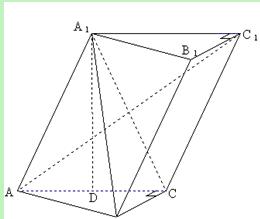
.若果数列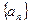 的项构成的新数列
的项构成的新数列 是公比为
是公比为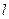 的等比数
的等比数 列,则相应的数列
列,则相应的数列 是公比为
是公比为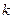 的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列
的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列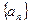 中,
中,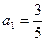 ,
, ,且
,且 .
.
(1)试利用双等比数列法求数列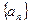 的通项公式;
的通项公式;
(2)求数列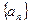 的前
的前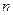 项和
项和
..已知函数 ,
,
(1)求函数 在
在 上的值域;
上的值域;
(2)在 中,若
中,若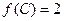 ,
, ,求
,求 .
.
.已知平面上三个向量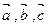 ,其中
,其中 ,
,
(1)若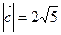 ,且
,且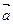 ∥
∥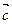 ,求
,求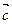 的坐标;
的坐标;
(2)若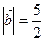 ,且
,且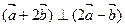 ,求
,求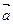 与
与 夹角的余弦值.
夹角的余弦值.
在三角形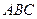 中,角
中,角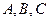 的对边分别是
的对边分别是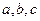 ,且
,且 ,
,
(1)求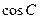 ;
;
(2)若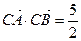 ,且
,且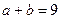 ,求
,求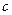 .
.
附加题(共3个小题每个小题5分)
1、已知x>y>0且xy=1, 的最小值是_____________
的最小值是_____________
2、已知点A(-3,5),B(0,3)试在直线y=x+1上找一点P使|PA |+|PB|最小求出最小值是
|+|PB|最小求出最小值是
3、数列 中,
中,
 ,
,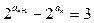 ,则通项
,则通项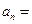 ;
;