(本小题满分13分)
已知数列 满足
满足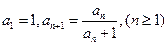 ,数列
,数列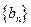 满足
满足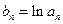 ,数列
,数列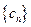
满足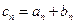 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ) ,
,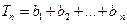 ,试比较
,试比较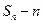 与
与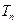 的大小,并证明;
的大小,并证明;
(Ⅲ)我们知道数列 如果是等差数列,则公差
如果是等差数列,则公差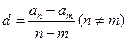 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列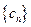 中,
中,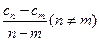 不是一个常数,但
不是一个常数,但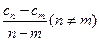 是否会小于等于一个常数
是否会小于等于一个常数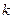 呢,若会,请求出
呢,若会,请求出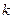 的范围,若不会,请说明理由.
的范围,若不会,请说明理由.
(本小题满分12分)已知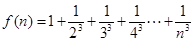 ,
,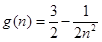 ,
,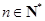 .
.
(1)当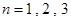 时,试比较
时,试比较 与
与 的大小关系;
的大小关系;
(2)猜想 与
与 的大小关系,并给出证明.
的大小关系,并给出证明.
(本小题满分12分)已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用P是多少元?
(2)设该厂 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这 天中用于配料的总费用
天中用于配料的总费用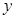 (元)关于
(元)关于 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
(本小题满分12分)设数列{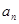 }的前n项和
}的前n项和 满足:
满足: =n
=n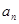 -2n(n-1).等比数列{
-2n(n-1).等比数列{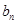 }的前n项和为
}的前n项和为 ,公比为
,公比为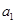 ,且
,且 =
=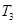 +2
+2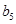 .
.
(1)求数列{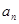 }的通项公式;
}的通项公式;
(2)设数列{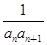 }的前n项和为
}的前n项和为 ,求证:
,求证: ≤
≤ <
<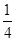 .
.
(本小题满分12分)直三棱柱ABC -A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
(Ⅰ)求证:AC⊥B1C;
(Ⅱ)若D是AB中点,求证:AC1∥平面B1CD;
(Ⅲ)当
 时,求二面角
时,求二面角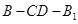 的余弦值.
的余弦值.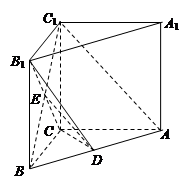
(本小题满分12分)已知向量m ,n
,n ,函数
,函数 m·n. (1)若
m·n. (1)若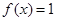 ,求
,求 的值;(2)在锐角△ABC中,角A,B,C的对边分别是
的值;(2)在锐角△ABC中,角A,B,C的对边分别是 ,且满足
,且满足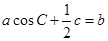 ,求
,求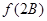 的取值范围.
的取值范围.