如图，在四棱锥P—ABCD中，PA⊥底面ABCD，底面为直角梯形，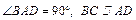
，且PA=AB=BC=1，AD=2．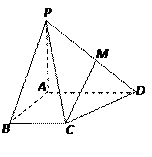
（Ⅰ）设M为PD的中点，求证：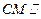
平面PAB；
（Ⅱ）求侧面PAB与侧面PCD所成二面角的平面角的正切值．
（本小题满分12分）已知二项式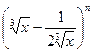
的展开式中，前三项系数的绝对
值成等差数列．
（I）求展开式的第四项；
（II）求展开式的常数项.
(本小题满分12分)已知函数f(x)=
,x∈［0，2］.
（1）求f(x)的值域；
（2）设a≠0,函数g(x)=
ax3-a2x,x∈［0，2］.若对任意x1∈［0，2］，总存在x2∈［0，2］，使f(x1)-g(x2)=0.求实数a的取值范围.
(本小题满分12分)设函数f（x）=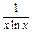
（x＞0且x≠1）.
（1）求函数f（x）的单调区间；
（2）已知2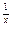
＞xa对任意x∈（0，1）成立，求实数a的取值范围.
(本小题满分12分)已知f(x)=ex-ax-1.
（1）求f(x)的单调增区间；
（2）若f(x）在定义域R内单调递增，求a的取值范围；
（3）是否存在a,使f(x)在（-∞，0］上单调递减，在［0，+∞）上单调递增？若存在，求出a的值；若不存在，说明理由.
(本小题满分12分)若函数y＝lg(3－4x＋x2)的定义域为M.当x∈M时，求f(x)＝2x＋2－3×4x的最值及相应的x的值．