（（本小题满分10分）选修4—4：作标系与参数方程
（1）已知点C 的极坐标为（2，
），画图并求出以C为圆心，半径r=2的圆的极坐标
方程（写出解题过程）；
（2）P是以原点为圆心，r=2的圆上的任意一点，Q（6，0），M是PQ中点
①画图并写出⊙O的参数方程；
②当点P在圆上运动时，求点M的轨迹的参数方程。
已知圆C：
内有一点P（2，2），过点P作直线l交圆C于A、B两点.
（1）当l经过圆心C时，求直线l的方程；
（2）当弦AB被点P平分时，写出直线l的方程；
（3）当直线l的倾斜角为45º时，求弦AB的长.
对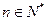
，不等式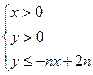
所表示的平面区域为
，把内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成一列点：
（1）求
，
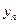
（2）若
（
为非零常数），问是否存在整数，使得对任意，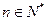
都有
．
设
,其导函数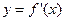
的图像经过点
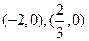,且在
时取得极小值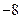
，
（1）求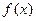
的解析式；
（2）若对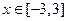
都有
恒成立，求实数
的取值范围。
如图，正三棱柱
的底面边长为
，侧棱长为
，点
在棱
上．
（1）若
，求证：直线
平面
；
（2）若
，二面角
平面角的大小为
，求
的值。
、
、
为
的三内角，且其对边分别为a、b、c，若
，
，且
．
（1）求角；
（2）若
，三角形面积
，求
的值．