(本小题满分14分)已知各项均不为零的数列{an}的前n项和为Sn,且满足a1=c,
2Sn=an an+1+r.
(1)若r=-6,数列{an}能否成为等差数列?若能,求 满足的条件;若不能,请说明理由;
满足的条件;若不能,请说明理由;
(2)设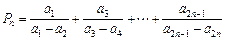 ,
, ,
,
若r>c>4,求证:对于一切n∈N*,不等式 恒成立.
恒成立.
(本小题满分12分)
某分公司经销某种产品,每件产品的成本为3元,并且每件产品需向总公司交纳6元的管理费,预计当每件产品的售价为x元(9 ≤ x ≤ 11)时,一年的销售量为 万件。(Ⅰ)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
万件。(Ⅰ)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,分公司一年的利润L最大?
(本小题满分12分)
已知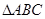 是复平面内的三角形,
是复平面内的三角形, 两点对应的复数分别为
两点对应的复数分别为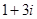 和
和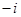 ,且
,且 ,
,
(Ⅰ)求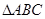 的顶点C的轨迹方程。
的顶点C的轨迹方程。
(Ⅱ)若复数 满足
满足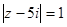 ,探究复数
,探究复数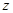 对应的点
对应的点 的轨迹与顶点C的轨迹的位置关系。
的轨迹与顶点C的轨迹的位置关系。
(本小题满分10分)
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
| 年份200x(年) |
0 |
1 |
2 |
3 |
4 |
| 人口数 y (十万) |
5 |
7 |
8 |
11 |
19 |
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出 y 关于x的线性回归方程;
(Ⅲ)据此估计2005年该城市人口总数。
参考数值:0×5+1×7+2×8+3×11+4×19=132,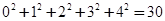 ,
,
参考公式: 用最小二乘法求线性回归方程系数公式 
(本小题满分6分)
已知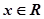 ,
,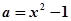 ,
, 。求证
。求证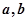 中至少有一个是非负数。
中至少有一个是非负数。
(本小题满分14分)规定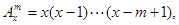 其中x∈R,m为正整数,且
其中x∈R,m为正整数,且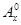 =1,这是排列数A
=1,这是排列数A (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.
(1)求A 的值;(2)确定函数
的值;(2)确定函数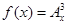 的单调区间.
的单调区间.
(3) 若关于 的方程
的方程 只有一个实数根, 求
只有一个实数根, 求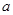 的值.
的值.