（本小题满分12分）（注意：在试题卷上作答无效）
函数
，其图象在
处的切线方程为
．
（Ⅰ）求函数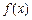
的解析式；
（Ⅱ）若函数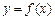
的图象与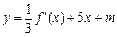
的图象有三个不同的交点，求实数
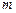的取值范围；
（Ⅲ）是否存在点P，使得过点P的直线若能与曲线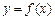围成两个封闭图形，则这两个封闭图形的面积相等？若存在，求出P点的坐标；若不存在，说明理由．
如图所示，在四棱锥P—ABCD中，底面ABCD是边长为a的正方形，E、F分别为PC、BD的中点，侧面PAD⊥底面ABCD，且PA＝PD＝
AD．
(1)求证：EF∥平面PAD；
(2)求证：平面PAB⊥平面PCD．
已知数列{an}是等差数列，且a3＝5，a2＋a7＝16.
(1)求数列{an}的通项公式；
(2)设bn＝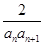
，求数列{bn}的前
项和Sn．
已知函数f(x)＝log4(2x＋3－x2)．
(1)求f(x)的定义域；
(2) 求f(x)的单调区间．
已知函数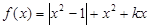
，且定义域为（0，2）.
(1）求关于x的方程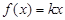
+3在（0，2）上的解；
（2）若
是定义域(0，2)上的单调函数，求实数
的取值范围；
（3）若关于x的方程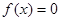
在（0，2）上有两个不同的解
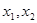，求k的取值范围。
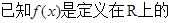单调函数，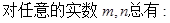
.
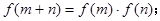
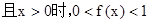（1）证明：f(0)=1且x<0时f(x)>1;
（2）