已知向量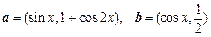 ,定义函数
,定义函数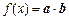
(I)求函数 最小正周期;
最小正周期;
(II)在△ABC中,角A为锐角,且 ,求边AC的长.
,求边AC的长.
已知集合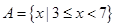 ,
,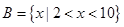 ,
,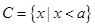 .
.
(1)求 ;
;
(2)若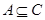 ,求实数
,求实数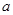 的取值范围.
的取值范围.
已知函数 (
(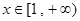 且
且 ).
).
(Ⅰ)用定义证明函数 在
在 上为增函数;
上为增函数;
(Ⅱ)设函数 ,若[2, 5 ]是
,若[2, 5 ]是 的一个单调区间,且在该区间上
的一个单调区间,且在该区间上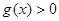 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
已知椭圆C的中心为坐标原点,长轴长为4,一条准线方程为
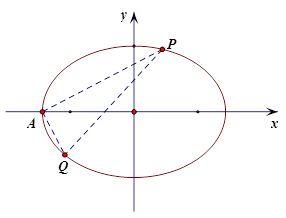
(1)求椭圆C的标准方程;
(2)求椭圆C被直线y=x+1截得的弦长;
(3)已知点A为椭圆的左顶点,过点A作斜率为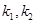 的两条直线与椭圆分别交于点P,Q,若
的两条直线与椭圆分别交于点P,Q,若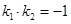 ,证明:直线PQ过定点,并求出定点的坐标.
,证明:直线PQ过定点,并求出定点的坐标.
已知圆 ,直线
,直线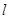 过定点A(1,0)
过定点A(1,0)
(1)若直线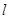 平分圆的周长,求直线
平分圆的周长,求直线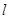 的方程;
的方程;
(2)若直线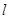 与圆相切,求直线
与圆相切,求直线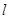 的方程;
的方程;
(3)若直线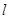 与圆C交于PQ两点,求△CPQ面积的最大值,并求此时的直线方程.
与圆C交于PQ两点,求△CPQ面积的最大值,并求此时的直线方程.
已知命题p:“方程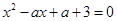 有解”,q:“
有解”,q:“ 上恒成立”,若p或q为真命题,p且q为假命题,求实数
上恒成立”,若p或q为真命题,p且q为假命题,求实数 的取值范围.
的取值范围.