已知椭圆 :
: (
( )的离心率
)的离心率 ,左、右焦点分别为
,左、右焦点分别为 、
、 ,点
,点 满足:
满足: 在线段
在线段 的中垂线上.
的中垂线上.
(1)求椭圆 的方程;
的方程;
(2)若斜率为 (
(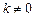 )的直线
)的直线 与
与 轴、椭圆
轴、椭圆 顺次相交于点
顺次相交于点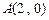 、
、 、
、 ,且
,且 ,求
,求 的取值范围.
的取值范围.
(本小题10分)
已知集合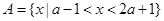 ,
,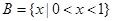 ,若
,若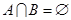 ,求实数a的取值范围.
,求实数a的取值范围.
(满分14分)已知定义在正实数集上的函数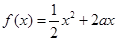 ,
,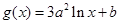 ,其中
,其中 .
.
设两曲线 ,
, 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用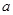 表示
表示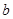 ;
;
(2)试证明不等式: (
( ).
).
(满分12分)如图,在直线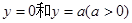 之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校.已知船速为
之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校.已知船速为 ,车速为
,车速为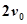 (水流速度忽略不计).若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间.
(水流速度忽略不计).若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间.
(满分12分)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥平面A1BD;
(2)求二面角A-A1D-B的余弦值;
(3)求点C1到平面A1BD的距离.
(满分12分)函数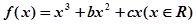 ,已知
,已知 是奇函数.
是奇函数.
(1)求b,c的值;
(2)求g(x)的单调区间与极值.