已知圆M的圆心在直线 上,且过点
上,且过点 、
、 .
.
(1)求圆M的方程;
(2)设P为圆M上任一点,过点P向圆O: 引切线,切点为Q.试探究:
引切线,切点为Q.试探究:
平面内是否存在一定点R,使得 为定值?若存在,求出点R的坐标;若不存在,请说
为定值?若存在,求出点R的坐标;若不存在,请说
明理由.
已知向量
 ,
, ,
,
 ,
, .
.
(1)求 与
与 的夹角;
的夹角;
(2)若




 ,求实数
,求实数 的值.
的值.
已知函数 ,其中
,其中 是常数.
是常数.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若 在定义域内是单调递增函数,求
在定义域内是单调递增函数,求 的取值范围;
的取值范围;
(Ⅲ)若关于 的方程
的方程 在
在 上有两个不相等的实数根,求
上有两个不相等的实数根,求 的取值范围.
的取值范围.
如图,直四棱柱 的底面
的底面 是平行四边形,
是平行四边形, ,
,  ,
, ,点
,点 是
是  的中点,点
的中点,点 在
在 且
且 .
.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求锐二面角 平面角的余弦值.
平面角的余弦值.
在数列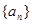 中,
中,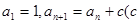 为常数,
为常数,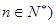 ,
,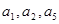 构成公比不等
构成公比不等
于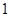 的等比数列.记
的等比数列.记 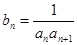 (
(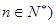 .
.
(Ⅰ)求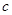 的值;
的值;
(Ⅱ)设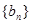 的前
的前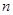 项和为
项和为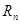 ,是否存在正整数
,是否存在正整数 ,使得
,使得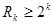 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
观察下列等式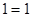 第一个式子
第一个式子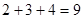 第二个式子
第二个式子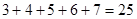 第三个式子
第三个式子 第四个式子
第四个式子
照此规律下去
(Ⅰ)写出第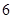 个等式;
个等式;
(Ⅱ)你能做出什么一般性的猜想?请用数学归纳法证明猜想.