已知命题p：关于x的方程x2+ax+a=0有实数解；命题q：﹣1＜a≤2．
（1）若¬p是真命题，求实数a的取值范围；
（2）若（¬p）∧q是真命题，求实数a的取值范围．
已知
（Ⅰ）若
求
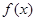的单调递减区间；
（Ⅱ）若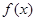在区间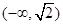
上单调递增，求
的取值范围．
计算：
（Ⅰ）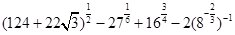
；
（Ⅱ）
如图，长方体的长、宽、高分别为4、3、5，已知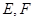
分别为线段
的中点．
（1）求证：
；
（2）求多面体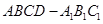
的体积．
某市“招手即停”公共汽车的票价按下列规则制定：
（1）5公里以内（含5公里），票价2元；
（2）5公里以上，每增加5公里，票价增加1元（不足5公里的按5公里计算）．
若某条线路的总里程为20公里，写出票价与里程之间的函数关系式，并求乘车16公里的票价．
己知⊙O：x2 +y2=6，P为⊙O上动点，过P作PM⊥x轴于M，N为PM上一点，且
．
（1）求点N的轨迹C的方程；
（2）若A（2，1），B（3，0），过B的直线与曲线C相交于D、E两点，则kAD+kAE是否为定值？若是，求出该值；若不是，说明理由．