(本小题满分12分)在△OAB中,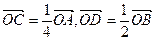 ,AD与BC交于点M,设
,AD与BC交于点M,设 =a,
=a, =b,
=b,
(1)用a,b表示 ;
;
(2)在线段AC上取一点E,在线段BD上取一点F,使EF过M点,设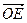 =p
=p ,
, =q
=q ,求证:
,求证: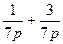 =1.
=1.
|
如图,在平面直角坐标系 中,以
中,以 轴为始边作两个锐角
轴为始边作两个锐角 ,它们的终边分别与单位圆交于
,它们的终边分别与单位圆交于 两点.已知
两点.已知 的横坐标分别为
的横坐标分别为 .
.
 的值;
的值;
 的值.
的值.

(满分14分)
已知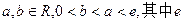 是自然对数的底数。
是自然对数的底数。
(1)试猜想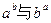 的大小关系;
的大小关系;
(2)证明你的结论。
(满分12分)
已知函数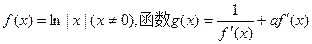
①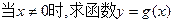 的表达式;
的表达式;
②当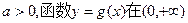 上的最小值是2,求a的值;
上的最小值是2,求a的值;
③在(2)的条件下,求直线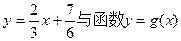 的图象所围成图形的面积。
的图象所围成图形的面积。
(满分12分)
已知 的展开式中x的系数为19,求
的展开式中x的系数为19,求 的展式式中
的展式式中 的系数的最小值。
的系数的最小值。
(满分12分)
某大学毕业生参加某单位的应聘考试,考核依次分为笔试,面试、实际操作共三轮进行,规定只有通过前一轮考核才能进入下一轮考核,否则被淘汰,三轮考核都通过才能被正式录用,设该大学毕业生通过一、二、三轮考核的概率分别为 ,且各轮考核通过与否相互独立。
,且各轮考核通过与否相互独立。
①求该大学毕业生进入第三轮考核的概率;
②设该大学毕业生在应聘考核中考核轮数为X,求X的概率分布列及期望和方差。