如图,PA垂直于矩形ABCD所在的平面,PD=PA,E、F分别是AB、PD的中点。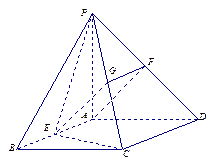
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD。
设圆 与圆
与圆 ,动圆C与圆
,动圆C与圆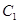 外切,与圆
外切,与圆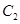 内切.
内切.
(1)求动圆C的圆心轨迹L的方程;
(2)已知点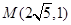 ,P为L上动点,求
,P为L上动点,求 最小值.
最小值.
平面直角坐标系 中,已知椭圆
中,已知椭圆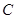 :
: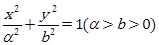 的离心率为
的离心率为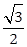 ,且点(
,且点(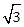 ,
, )在椭圆
)在椭圆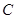 上.
上.
(Ⅰ)求椭圆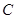 的方程;
的方程;
(Ⅱ)设椭圆 :
: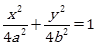 ,
, 为椭圆
为椭圆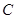 上任意一点,过点
上任意一点,过点 的直线
的直线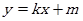 交椭圆
交椭圆 于
于 两点,射线
两点,射线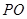 交椭圆
交椭圆 于点
于点 .
.
(i)求 的值;
的值;
(ii)求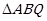 面积的最大值.
面积的最大值.
已知函数
(I)求 的单调区间;
的单调区间;
(II)设曲线 与
与 轴正半轴的交点为P,曲线在点P处的切线方程为
轴正半轴的交点为P,曲线在点P处的切线方程为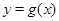 ,求证:对于任意的正实数
,求证:对于任意的正实数 ,都有
,都有 ;
;
(III)若方程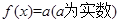 有两个正实数根
有两个正实数根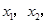 且
且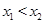 ,求证:
,求证: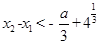 .
.
已知数列 中,
中,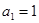 ,
,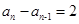 (
(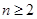 )
)
(I)求数列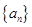 的通项公式和它的前
的通项公式和它的前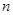 项和
项和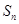 ;
;
(II)设 ,求数列
,求数列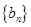 的前
的前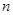 项和
项和 .
.
如图,已知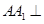 平面ABC,
平面ABC,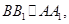 AB=AC=3,
AB=AC=3, ,,
,, 点E,F分别是BC,
点E,F分别是BC, 的中点.
的中点.
(I)求证:EF 平面
平面 ;
;
(II)求证:平面 平面
平面 .
.
(III)求直线 与平面
与平面 所成角的大小.
所成角的大小.