某饮料公司招聘一名员工，现对其进行一项测试，以便确定工资级别.公司准备了两种不同的饮料共8杯，其颜色完全相同，并且其中4杯为
饮料，另外4杯为
饮料，公司要求此员工一一品尝后，从8杯饮料中选出4杯
饮料.若4杯都选对，则月工资定为3500元；若4杯选对3杯，则月工资定为2800元；否则月工资定为2100元.令
表示此人选对
饮料的杯数.假设次人对
和
两种饮料没有鉴别能力.
（1）求
的分布列；
（2）求此员工月工资的期望.
(本小题满分10分)
已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和4个黑
球．现从甲、乙两个盒内各任取2个球.
（1）求取出的4个球均为黑球的概率；
（2）求取出的4个球中恰有1个红球的概率；
（3）设
为取出的4个球中红球的个数，求的分布列，并求其数学期望E（）.
（本小题满分10分）
如图，在四棱锥
中，底面ABCD为直角梯形，AB∥CD，∠BAD=90°，PA⊥平面ABCD，AB=1，AD=2，PA=CD=4，求二面角
的余弦值.
D. ［选修4－5：不等式选讲］（本小题满分10分）
已知
是正数，证明：
.
C. ［选修4－4：坐标系与参数方程］（本小题满分10分）
已知直线
的参数方程：
（
为参数）和圆C的极坐标方程：
，判断直线和⊙C的位置关系.
B. ［选修4－2：矩阵与变换］（本小题满分10分）
已知二阶矩阵A的属于特征值－1的一个特征向量为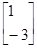
，属于特征值3的一个特征向量为
，求矩阵A.