是双曲线
:
上一点,
分别是双曲线
的左、右定点,直线
的斜率之积为
.
(1)求双曲线的离心率;
(2)过双曲线
的右焦点且斜率为1的直线交双曲线于
两点,
为坐标原点,
为双曲线上的一点,满足
,求
的值.
(本小题满分12分)
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 在区间
在区间 上的取值范围.
上的取值范围.
设函数
(Ⅰ)当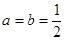 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)令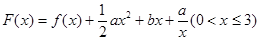 其图象上任意一点
其图象上任意一点 处切线的斜率
处切线的斜率 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)当 ,
, 时,方程
时,方程 在区间
在区间 内有唯一实数解,求实数
内有唯一实数解,求实数 的取值范围.
的取值范围.
定义在R上的奇函数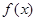 有最小正周期4,且
有最小正周期4,且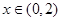 时,
时,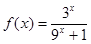 .
.
(1)求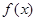 在
在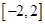 上的解析式;
上的解析式;
(2)判断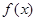 在
在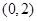 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当 为何值时,关于方程
为何值时,关于方程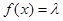 在
在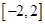 上有实数解?
上有实数解?
某同学用“五点法”画函数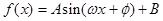 (
( )在某一个周期内的图象时,列表并填入的部分数据如下表:
)在某一个周期内的图象时,列表并填入的部分数据如下表:
 |
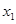 |
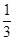 |
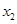 |
 |
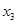 |
 |
 |
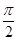 |
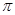 |
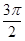 |
 |
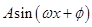 |
 |
 |
 |
 |
 |
(Ⅰ)请求出上表中的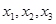 ,并直接写出函数
,并直接写出函数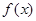 的解析式;
的解析式;
(Ⅱ)将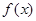 的图象沿x轴向右平移
的图象沿x轴向右平移 个单位得到函数
个单位得到函数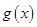 ,若函数
,若函数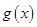 在
在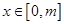 (其中
(其中 上的值域为
上的值域为 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为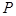 、
、 ,求
,求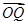 与
与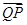 夹角θ的大小.
夹角θ的大小.
学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数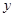 与听课时间
与听课时间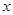 (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点 ,过点
,过点 ;当
;当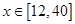 时,图象是线段
时,图象是线段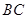 ,其中
,其中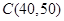 .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.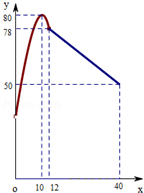
(1)试求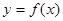 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.