学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数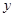 与听课时间
与听课时间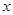 (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点 ,过点
,过点 ;当
;当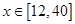 时,图象是线段
时,图象是线段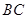 ,其中
,其中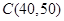 .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.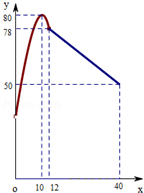
(1)试求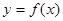 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
(1)求数列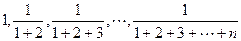 的通项公式
的通项公式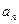
(2)求数列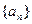 的前n项和
的前n项和
(本小题满分14分)
已知数列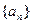 ,
,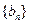 满足
满足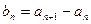 ,其中
,其中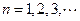 .
.
(Ⅰ)若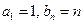 ,求数列
,求数列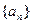 的通项公式;
的通项公式;
(Ⅱ)若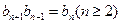 ,且
,且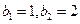 .
.
(ⅰ)记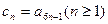 ,求证:数列
,求证:数列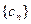 为等差数列;
为等差数列;
(ⅱ)若数列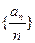 中任意一项的值均未在该数列中重复出现无数次. 求首项
中任意一项的值均未在该数列中重复出现无数次. 求首项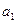 应满足的条件.
应满足的条件.
(本小题满分14分)
已知函数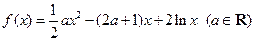 .
.
(Ⅰ)若曲线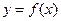 在
在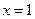 和
和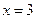 处的切线互相平行,求
处的切线互相平行,求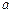 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设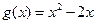 ,若对任意
,若对任意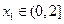 ,均存在
,均存在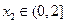 ,使得
,使得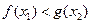 ,求
,求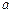 的取值范围.
的取值范围.
(本小题满分13分)
已知椭圆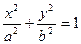 (
(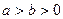 )的右焦点为
)的右焦点为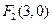 ,离心率为
,离心率为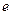 .
.
(Ⅰ)若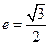 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设直线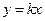 与椭圆相交于
与椭圆相交于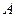 ,
,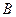 两点,
两点,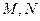 分别为线段
分别为线段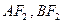 的中点. 若坐标原点
的中点. 若坐标原点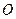 在以
在以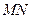 为直径的圆上,且
为直径的圆上,且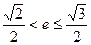 ,求
,求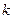 的取值范围.
的取值范围.
(本小题满分13分)
一个袋中装有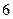 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为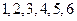 .
.
(Ⅰ)若从袋中每次随机抽取1个球,有放回的抽取2次,求取出的两个球编号之和为6的概率;
(Ⅱ)若从袋中每次随机抽取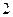 个球,有放回的抽取3次,求恰有
个球,有放回的抽取3次,求恰有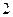 次抽到
次抽到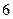 号球的概率;
号球的概率;
(Ⅲ)若一次从袋中随机抽取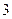 个球,记球的最大编号为
个球,记球的最大编号为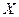 ,求随机变量
,求随机变量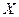 的分布列.
的分布列.