某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共
杯,其颜色完全相同,并且其中
杯为
饮料,另外
杯为
饮料,公司要求此员工一一品尝后,从
杯饮料中选出
杯
饮料.若该员工
杯都选对,则评为优秀;若3杯选对
杯,则评为良好;否则评为及格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
在1与2之间插入 个正数
个正数 ,使这
,使这 个数成等比数列;又在1与2之间插入
个数成等比数列;又在1与2之间插入 个正数
个正数 ,使这
,使这 个数成等差数列.记
个数成等差数列.记 .求:
.求:求数列
 和
和 的通项;
的通项;当
 时,比较
时,比较 与
与 的大小,并证明你的结论
的大小,并证明你的结论
设数列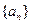 满足
满足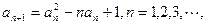
当
 时,求
时,求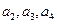 ,并由此猜想出
,并由此猜想出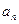 的一个通项公式;
的一个通项公式;当
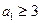 时,证明对所有的
时,证明对所有的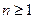 ,有(ⅰ)
,有(ⅰ)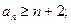
(ⅱ)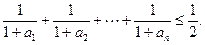
设 为常数,且
为常数,且
证明对任意

假设对任意
 有
有 ,求
,求 的取值范围.
的取值范围.
试判断下面的证明过程是否正确:
用数学归纳法证明:
证明:(1)当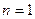 时,左边=1,右边=1
时,左边=1,右边=1
∴当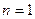 时命题成立.
时命题成立.
(2)假设当 时命题成立,即
时命题成立,即
则当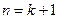 时,需证
时,需证
由于左端等式是一个以1为首项,公差为3,项数为 的等差数列的前
的等差数列的前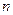 项和,其和为
项和,其和为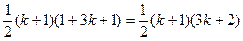
∴ 式成立,即
式成立,即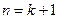 时,命题成立.根据(1)(2)可知,对一切
时,命题成立.根据(1)(2)可知,对一切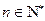 ,命题成立.
,命题成立.
试判断下面的证明过程是否正确:
用数学归纳法证明: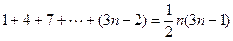
证明:(1)当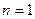 时,左边=1,右边=1
时,左边=1,右边=1
∴当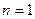 时命题成立.
时命题成立.
(2)假设当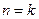 时命题成立,即
时命题成立,即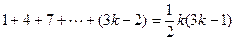
则当 时,需证
时,需证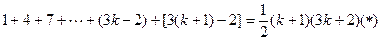
由于左端等式是一个以1为首项,公差为3,项数为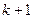 的等差数列的前
的等差数列的前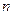 项和,其和为
项和,其和为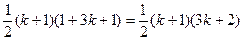
∴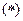 式成立,即
式成立,即 时,命题成立.根据(1)(2)可知,对一切
时,命题成立.根据(1)(2)可知,对一切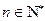 ,命题成立.
,命题成立.