如图,四棱锥 中,底面 为平行四边形, 底面 .
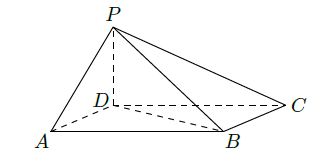
(1)证明: ;
(2)设 ,求棱锥 的高.
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF 平面EFDC.
平面EFDC.
(Ⅰ)当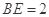 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点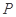 ,且
,且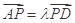 ,使得CP∥平面ABEF?若存在,求出
,使得CP∥平面ABEF?若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ)设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.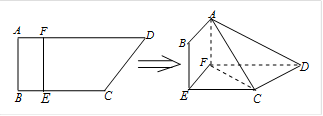
已知曲线C:
(1)当 为何值时,曲线C表示圆;
为何值时,曲线C表示圆;
(2)在(1)的条件下,若曲线C与直线 交于M、N两点,且
交于M、N两点,且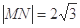 ,求
,求 的值.
的值.
(3)在(1)的条件下,设直线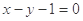 与圆
与圆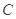 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得以
,使得以 为直径的圆过原点,若存在,求出实数
为直径的圆过原点,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.
(1)求证:
(2)求证:DE∥平面PBC;
已知一个几何体的三视图如图所示.
(Ⅰ)求此几何体的表面积;
(Ⅱ)在如图的正视图中,如果点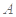 为所在线段中点,点
为所在线段中点,点 为顶点,求在几何体侧面上从点
为顶点,求在几何体侧面上从点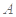 到点
到点 的最短路径的长.
的最短路径的长.
已知圆 :
: 内有一点
内有一点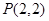 ,过点
,过点 作直线
作直线 交圆
交圆 于
于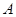 ,
, 两点.
两点.
(Ⅰ)当 经过圆心
经过圆心 时,求直线
时,求直线 的方程;
的方程;
(Ⅱ)当弦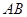 被点
被点 平分时,写出直线
平分时,写出直线 的方程.
的方程.