在平面直角坐标系中,曲线
与坐标轴的交点都在圆
上,
(1)求圆
的方程;
(2)如果圆
与直线
交于
两点,且
,求
的值.
(本小题满分14分)某汽车厂有一条价值为 万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值.经过市场调查,产品的增加值
万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值.经过市场调查,产品的增加值 万元与技术改造投入的
万元与技术改造投入的 万元之间满足:①
万元之间满足:① 与
与 和
和 的乘积成正比;②
的乘积成正比;② ,其中
,其中 是正常数.若
是正常数.若 时,
时,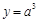 .
.
(Ⅰ)求产品增加值 关于
关于 的表达式;
的表达式;
(Ⅱ)求产品增加值 的最大值及相应的
的最大值及相应的 的值.
的值.
(本小题满分14分)如图,在三棱柱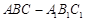 中,
中,  ,侧面
,侧面 是矩形,
是矩形, 分别是
分别是 的中点.
的中点.
(Ⅰ)证明: 面
面 ;
;
(Ⅱ)证明:面 面
面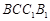 .
.
(本小题满分14分)已知函数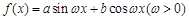 的图像过点
的图像过点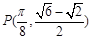 且关于直线
且关于直线 对称,图像上相邻两个最高点的距离为
对称,图像上相邻两个最高点的距离为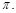
(Ⅰ)求 的值;
的值;
(Ⅱ)若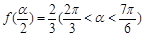 ,求
,求 的值.
的值.
(本小题满分14分)已知函数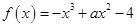 ,
,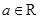 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若存在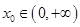 ,使
,使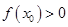 ,求实数
,求实数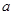 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆 的两个焦点分别为
的两个焦点分别为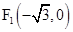 ,
,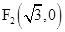 ,点
,点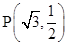 在椭圆
在椭圆
上.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)在椭圆 落在第一象限的图象上任取一点作
落在第一象限的图象上任取一点作 的切线
的切线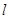 ,求
,求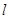 与坐标轴围成的三角形的面积的最小
与坐标轴围成的三角形的面积的最小
值;
(Ⅲ)设椭圆 的左、右顶点分别为
的左、右顶点分别为 ,
,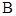 ,过椭圆
,过椭圆 上的一点
上的一点 作
作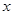 轴的垂线交
轴的垂线交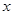 轴于点
轴于点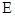 ,若
,若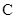 点
点
满足 ,
,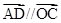 ,连结
,连结 交
交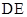 于点
于点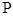 ,求证:
,求证: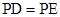 .
.