(本小题满分14分)已知椭圆 的两个焦点分别为
的两个焦点分别为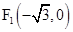 ,
,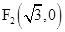 ,点
,点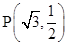 在椭圆
在椭圆
上.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)在椭圆 落在第一象限的图象上任取一点作
落在第一象限的图象上任取一点作 的切线
的切线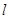 ,求
,求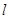 与坐标轴围成的三角形的面积的最小
与坐标轴围成的三角形的面积的最小
值;
(Ⅲ)设椭圆 的左、右顶点分别为
的左、右顶点分别为 ,
,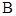 ,过椭圆
,过椭圆 上的一点
上的一点 作
作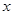 轴的垂线交
轴的垂线交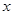 轴于点
轴于点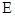 ,若
,若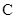 点
点
满足 ,
,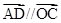 ,连结
,连结 交
交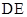 于点
于点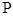 ,求证:
,求证: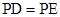 .
.
(本小题满分12分)已知曲线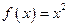 .
.
(1)求曲线 在(1,1)点处的切线
在(1,1)点处的切线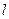 的方程;
的方程;
(2)求由曲 线
线 、直线
、直线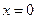 和直线
和直线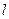 所围成图形的面积。
所围成图形的面积。
(本小题满分14分)
设圆满足条件:(1)截y轴所得的弦长为2;(2)被x轴分成两段弧,其弧长的比为3︰1;(3)圆心到直线 :
: 的距离为
的距离为 .求这个圆的方程.
.求这个圆的方程.
(本 小题满分12分)
小题满分12分)
已知点A(15,0),点P是圆 上的动点,M为线段PA的中点,当点P在圆上运动时,求动点M的轨迹方程.
上的动点,M为线段PA的中点,当点P在圆上运动时,求动点M的轨迹方程.
、(本小题满分12分)
我校高一有A,B,C三科兴趣小组,用分层抽样方法从参加这三科的同学中,抽取若干人组成一个队,代表我校参加德州市组织的科技竞赛活动,有关数据见下表(单位:人)
| 科目 |
人数 |
抽取人数 |
| A |
18 |
x |
| B |
36 |
2 |
| C |
54 |
y |
(1)求x,y ;
(2)若从B、C两科抽取的人中选2人参加市队, 求这二人都来自C科的概率.
求这二人都来自C科的概率.
 |
(本小题满分12分)
设集合A={1,2,3,4,5},集合B={1,2, 3},在A中任取一个数为x,在B中任取一个数为y,组成点(x,y).
(1)写出基本事件空间;
(2)求事件 “x
“x y为偶数”的概率;
y为偶数”的概率;
(3)求事件“xy为奇数”的概率.