如图,已知椭圆
的中心在原点
,长轴左、右端点
在
轴上,椭圆
的短轴为
,且
的离心率都为
,直线
,
交于两点,与
交于两点,这四点按纵坐标从大到小依次为
.
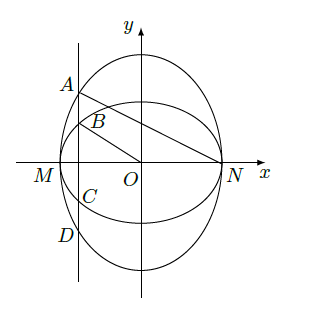
(1)设
,求
与
的比值;
(2)当
变化时,是否存在直线
,使得
,并说明理由.
如图,已知抛物线 :
: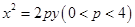 ,其上一点
,其上一点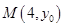 到其焦点
到其焦点 的距离为
的距离为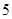 ,过焦点
,过焦点 的直线
的直线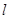 与抛物线
与抛物线 交于
交于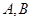 左、右两点.
左、右两点.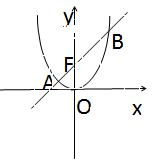
(Ⅰ)求抛物线 的标准方程;
的标准方程;
(Ⅱ)若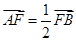 ,求直线
,求直线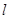 的方程.
的方程.
已知圆 的半径为
的半径为 ,圆心
,圆心 在直线
在直线 上.
上.
(Ⅰ)若圆 被直线
被直线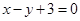 截得的弦长为
截得的弦长为 ,求圆
,求圆 的标准方程;
的标准方程;
(Ⅱ)设点 ,若圆
,若圆 上总存在两个点到点
上总存在两个点到点 的距离为
的距离为 ,求圆心
,求圆心 的横坐标
的横坐标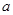 的取值范围.
的取值范围.
已知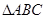 的三个顶点的坐标为
的三个顶点的坐标为 .
.
(Ⅰ)求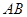 边上的高所在直线的方程;
边上的高所在直线的方程;
(Ⅱ)若直线 与
与 平行,且在
平行,且在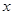 轴上的截距比在
轴上的截距比在 轴上的截距大
轴上的截距大 ,求直线
,求直线 与两条坐标轴围成的三角形的周长.
与两条坐标轴围成的三角形的周长.
在边长为4的正方形ABCD的边上有一点P沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
(1)写出框图中①、②、③处应填充的式子;
(2)若输出的面积y值为6,则路程x的值为多少?并指出此时点P的在正方形的什么位置上?
已知p:关于x的方程 的两根均大于3,q:A={x|x2﹣2x+a>0}且1∉A,
的两根均大于3,q:A={x|x2﹣2x+a>0}且1∉A,
(1)求使p成立的充要条件;
(2)若p∨q为真命题,求实数a的取值范围.