在数列{an}中,a1=1,an+1= (n∈N*).
(Ⅰ)求a2,a3,a4;
(Ⅱ)猜想an;(不用证明)
设函数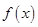 对任意
对任意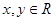 ,都有
,都有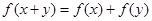 ,当
,当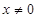 时,
时,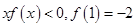
(1)求证: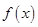 是奇函数;
是奇函数;
(2)试问:在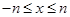 时
时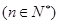 ,
,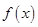 是否有最大值?如果有,求出最大值,如果没有,说明理由.
是否有最大值?如果有,求出最大值,如果没有,说明理由.
(3)解关于x的不等式

(1)求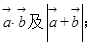
(2) .
.
已知函数 的图象在与
的图象在与 轴交点处的切线方程是
轴交点处的切线方程是 .
.
(I)求函数 的解析式;
的解析式;
(II)设函数 ,若
,若 的极值存在,求实数
的极值存在,求实数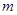 的取值范围以及函数
的取值范围以及函数 取得极值时对应的自变量
取得极值时对应的自变量 的值.
的值.
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是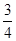 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.
(I)设该选手参赛的轮次为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)对于(I)中的 ,设“函数
,设“函数 是偶函数”为事件D,求事件D发生的概率.
是偶函数”为事件D,求事件D发生的概率.
函数 (A>0,
(A>0, >0)的最小值为-1,其图象相邻两个对称中心之间的距离为
>0)的最小值为-1,其图象相邻两个对称中心之间的距离为 .
.
(1)求函数 的解析式
的解析式
(2)设 ,则
,则 ,求
,求 的值.
的值.