设函数f(x)=ax-(a+1)ln(x+1),其中a>0.
(1)求f(x)的单调区间;
(2)当x>0时,证明不等式: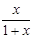 <ln(x+1)<x;
<ln(x+1)<x;
(3)设f(x)的最小值为g(a),证明不等式:-1<ag(a)<0
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.
已知 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
(1)证明:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前 项和
项和 .
.
设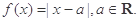
(1)当 ,解不等式
,解不等式 ;
;
(2)当 时,若
时,若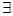
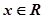 ,使得不等式
,使得不等式 成立,求实数
成立,求实数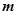 的取值范围.
的取值范围.
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线 的参数方程为
的参数方程为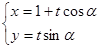 (t为参数,0<a<
(t为参数,0<a< ),曲线C的极坐标方程为
),曲线C的极坐标方程为 .
.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A、B两点,当a变化时,求|AB|的最小值.
如图,已知⊙O是 的外接圆,
的外接圆, 是
是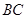 边上的高,
边上的高, 是⊙O的直径.
是⊙O的直径.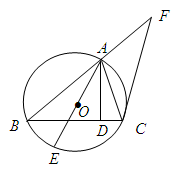
(1)求证: ;
;
(2)过点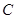 作⊙O的切线交
作⊙O的切线交 的延长线于点
的延长线于点 ,若
,若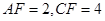 ,求
,求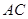 的长.
的长.