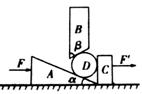
如图所示,质量为mB=14kg的木板B放在水平地面上,质量为mA=10kg的木箱A在木板B上。一根轻绳一端拴在木箱上,另一端拴在地面的木桩上,绳绷紧时与水平面的夹角为 =37°。已知木箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4。重力加速度g取10m/s2。现用水平力F将木板B从木箱A下面匀速抽出,试求:(sin37°=0.6,cos37°=0.8)
=37°。已知木箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4。重力加速度g取10m/s2。现用水平力F将木板B从木箱A下面匀速抽出,试求:(sin37°=0.6,cos37°=0.8)
(1)绳上张力T的大小;
(2)拉力F的大小。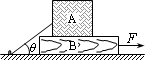
(10分)如图所示,斜面倾角为θ,质量为m的滑块距挡板P为s0,以初速度v0。沿斜面上滑。滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于滑块沿斜面的下滑力。若滑块每次与挡板相碰均无机械能损失。问滑块经过的路程有多大?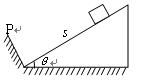
(10分)如图所示,一条小河两岸的高度差h=5m,一辆摩托车(可看作质点)以v 0=20m/s 的水平速度向河对岸飞出,恰好越过小河.不计空气阻力,取当地的重力加速度g=10m/s2。
试求:
(1)摩托车在空中的飞行时间;
(2)小河的宽度。
如图所示,物体A放在足够长的木板B上,木板B静止于水平面。t=0时,电动机通过水平细绳以恒力F拉木板B,使它做初速度为零,加速度aB=1.0m/s2的匀加速直线运动。已知A的质量mA和B的质量mg均为2.0kg,A、B之间的动摩擦因数μ1=0.05,B与水平面之间的动摩擦因数μ2=0.1,最大静摩擦力与滑动摩擦力大小视为相等,重力加速度g取10m/s2。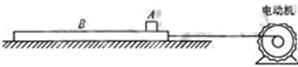
求:
(1)物体A刚运动时的加速度aA
(2)t=1.0s时,电动机的输出功率P;
(3)若t=1.0s时,将电动机的输出功率立即调整为P/=5W,并在以后的运动过程中始终保持这一功率不变,t=3.8s时物体A的速度为1.2m/s。则在t=1.0s到t=3.8s这段时间内木板B的位移为多少?
半径为R光滑球恰好放在木块的圆槽中,OA与水平成θ角,圆球质量为m,木块质量为M,不计摩擦,求:人手至少用多大恒力F垂直向下拉木块B端,球才可离槽?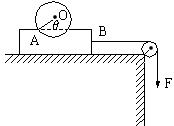
有一种机械装置叫做“滚珠式力放大器”,其原理如图所示,斜面A可以在水平面上滑动,斜面B以及物块C都是被固定的,它们均由钢材制成,钢珠D置于ABC之间。当用水平力F推斜面A时,钢珠D对物块C的挤压力F/就会大于F,故称为“滚珠式力放大器”。如果斜面A、B的倾角分别为α、β,不计一切摩擦力以及钢珠自身的重力,求这一装置的力放大倍数(即F/与F之比)