在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率 为0.25,在B处的命中率为
为0.25,在B处的命中率为 ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
 |
0 |
2 |
3 |
4 |
5 |
| p |
0.03 |
P1 |
P2 |
P3 |
P4 |
(1)求 的值;
的值;
(2)求随机变量 的数学期望
的数学期望 ;
;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
(本小题满分12分)已知关于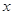 的函数
的函数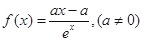
(1)当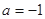 时,求函数
时,求函数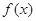 的极值;
的极值;
(2)若函数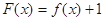 没有零点,求实数
没有零点,求实数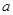 的取值范围.
的取值范围.
(本小题满分12分)设函数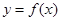 在
在 上的导函数为
上的导函数为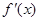 ,
,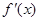 在
在 上的导函数为
上的导函数为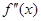 ,若在
,若在 上,
上,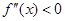 恒成立,则称函数
恒成立,则称函数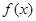 在
在 上为“凸函数”.已知
上为“凸函数”.已知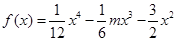 .
.
(1)若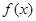 为区间
为区间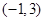 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数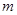 的值;
的值;
(2)若当实数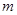 满足
满足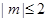 时,函数
时,函数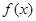 在
在 上总为“凸函数”,求
上总为“凸函数”,求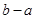 的最大值.
的最大值.
(本小题满分10分)已知函数
(1)若直线 与曲线
与曲线 相切,求实数
相切,求实数 的值;
的值;
(2)若 ,比较
,比较 与
与 的大小
的大小
(本小题满分12分)在锐角 中,已知内角
中,已知内角 、
、 、
、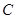 所对的边分别为
所对的边分别为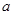 、
、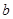 、
、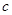 ,向量
,向量 ,且向量
,且向量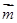 ,
, 共线.
共线.
(1)求角 的大小;
的大小;
(2)如果 ,求
,求 的面积
的面积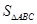 的最大值.
的最大值.
(本小题满分12分)已知函数 ,
,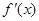 是
是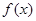 的导函数.
的导函数.
(1)求函数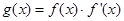 的最小值及相应的
的最小值及相应的 值的集合;
值的集合;
(2)若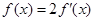 ,求
,求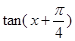 的值.
的值.