某小组6个人排队照相留念。(1)若分成两排照相,前排2人,后排4人,有多少种不同的排法?(2)若分成两排照相,前排2人,后排4人,但其中甲必须在前排,乙必须在后排,有多少种排法?(3)若排成一排照相,甲、乙两人必须在一起,有多少种不同的排法?(4)若排成一排照相,其中甲必在乙的右边,有多少种不同的排法?(5)若排成一排照相,其中有3名男生3名女生,且男生不能相邻有多少种排法?(6)若排成一排照相,且甲不站排头乙不站排尾,有多少种不同的排法?
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程
的参数方程 (
( 为参数).以
为参数).以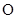 为极点,
为极点,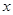 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)直线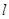 的极坐标方程是
的极坐标方程是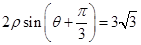 ,射线
,射线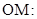
 与圆
与圆 的交点为
的交点为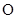 、
、 ,与直线
,与直线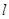 的交点为
的交点为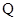 ,求线段
,求线段 的长.
的长.
(本小题满分10分)选修4—1:几何证明选讲
如图所示,已知圆 外有一点
外有一点 ,作圆
,作圆 的切线
的切线 ,
,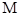 为切点,过
为切点,过 的中点
的中点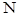 ,作割线
,作割线 ,交圆于
,交圆于 、
、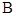 两点,连接
两点,连接 并延长,交圆
并延长,交圆 于点
于点 ,连接
,连接 交圆
交圆 于点
于点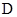 ,若
,若 .
.
(1)求证: ∽
∽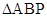 ;
;
(2)求证:四边形 是平行四边形.
是平行四边形.
(本小题满分12分)函数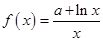 ,若曲线
,若曲线 在点
在点 处的切线与直线
处的切线与直线 垂直(其中
垂直(其中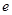 为自然对数的底数).
为自然对数的底数).
(1)若 在
在 上存在极值,求实数
上存在极值,求实数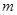 的取值范围;
的取值范围;
(2)求证:当 时,
时, .
.
(本小题满分12分)椭圆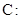
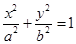 (
(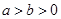 )的上顶点为
)的上顶点为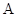 ,
,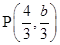 是
是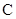 上的一点,以
上的一点,以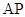 为直径的圆经过椭圆
为直径的圆经过椭圆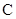 的右焦点
的右焦点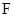 .
.
(1)求椭圆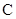 的方程;
的方程;
(2)动直线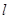 与椭圆
与椭圆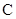 有且只有一个公共点,问:在
有且只有一个公共点,问:在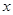 轴上是否存在两个定点,它们到直线
轴上是否存在两个定点,它们到直线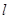 的距离之积等于
的距离之积等于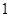 ?如果存在,求出这两个定点的坐标;如果不存在,说明理由.
?如果存在,求出这两个定点的坐标;如果不存在,说明理由.
(本小题满分12分)直三棱柱 中,
中,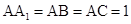 ,
,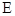 ,
,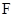 分别是
分别是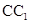 、
、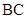 的中点,
的中点,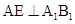 ,
,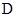 为棱
为棱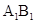 上的点.
上的点.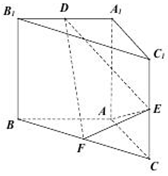
(1)证明: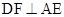 ;
;
(2)是否存在一点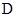 ,使得平面
,使得平面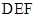 与平面
与平面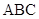 所成锐二面角的余弦值为
所成锐二面角的余弦值为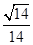 ?若存在,说明点
?若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.